In finance and mathematics, many scenarios require transitioning from a discrete model, such as a sum, to a continuous approximation, such as an integral. This transition simplifies calculations, models asymptotic behaviors, and generalizes results.
However, this transition comes with challenges, particularly in adjusting for differences between the two approaches. These adjustments often include specific corrections, such as those involving the fractional part of a continuous variable, which plays a key role in fine-tuning local discrepancies.
This article explores the general principle of this transition, its role, and the importance of the fractional part in correcting differences.
1. General Principle: Connecting Sums and Integrals
Discrete sums and continuous integrals are two ways of measuring a total quantity:
Continuous integrals capture the area under the curve by integrating the function over a continuous interval, for example:
To connect a discrete sum to a continuous integral, we use an approximation that includes:
- A main integral that captures the bulk of the sum.
- Corrective terms, such as those involving the fractional part, to adjust for local variations.
2. Role of Transitioning from Discrete to Continuous in Finance
This transition is especially useful in finance, where flows or data are often discrete. Here are some key examples:
- Option pricing: The price of an option, expressed as an expectation, relies on continuous integrals, even though prices evolve discretely.
- Cash flows: Periodic payments, such as bond coupons, can be replaced with continuous flows to simplify calculations.
- Risk measures: Metrics like Value-at-Risk (VaR) use continuous distributions, even when historical data is discrete.
Transitioning from discrete to continuous simplifies theoretical calculations and enables the use of more powerful analytical tools.
3. The Need for an Extended Step in the Integral
When replacing a sum with an integral, it is often useful to start the integral before the initial index of the sum.
For example:
Why start earlier?
- Global approximation: Starting at \( t = 1 \) (instead of \( t = 2 \)) extends the base of the integral, better capturing the global contributions of the function.
-
- Analytical simplicity: Starting the integral at \( t = 1 \) avoids treating specific cases at \( t = 2 \), making the calculations smoother.
4. The Role of the Fractional Part
The fractional part of \( t \), denoted \( \{t\} \), is essential for correcting local discrepancies between discrete and continuous approaches. It is defined as:
where \( \lfloor t \rfloor \) is the integer part of \( t \).
Correction Using the Fractional Part
In the relationship between sums and integrals, a corrective term involving \( \{t\} \) is included:
- Adding local variations: The fractional part \( \{t\} \) measures the difference between \( t \) (continuous) and its previous integer. This adjusts for the missing discrete contributions.
- Managing oscillations: If \( f(t) \) oscillates rapidly, such as with \( \cos(\ln t) \), the term \( \{t\} f'(t) \) adjusts these oscillations to align the sum and the integral.
[1] The term \( \{t\} f'(t) \) is a local correction that adjusts the transition between the discrete sum and the continuous integral:
- \( f'(t) \): The derivative of the function \( f(t) \), representing the local variation of \( f \) around \( t \).
- \( \{t\} \): Measures how far \( t \) is from its previous integer, weighting this correction accordingly.
This product adjusts for the small differences left by transitioning from discrete to continuous.

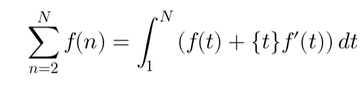
Écrire commentaire