Advanced algorithms enable computers to identify patterns, make decisions, and even predict the future based on data. Among these powerful tools, the Support Vector Machine (SVM) is notable for its effectiveness, especially in the field of classification.
But how does it work?
Let's demystify this algorithm, starting with one of its fundamental concepts: the hyperplane.
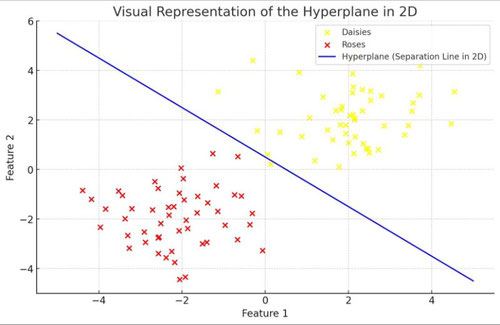
Imagine you're at a park and you observe a wide, open field with various types of flowers scattered all around. Your task is to draw a straight line that separates two types of flowers, say daisies and roses, so that all the daisies end up on one side of the line and all the roses on the other. In two dimensions, like our field, this line is akin to what mathematicians call a "hyperplane."
In the context of SVM, we're often not working with fields and flowers but with data points in spaces that can have many dimensions beyond just two. If we were dealing with three types of characteristics (like the size, color, and smell of flowers), we would be in a three-dimensional space, and our "line" would actually be a flat sheet that divides the space into two parts. This flat sheet is described mathematically as (ax + by + cz + d = 0), where (a), (b), and (c) are coefficients that define the orientation of the plane in three-dimensional space, and (d) is the offset from the origin.
As we increase the dimensions, our hyperplane remains the thing that cleanly separates our data into two categories, but it becomes harder to visualize.
The hyperplane is the heart of the SVM algorithm. The aim of SVM is to find the best hyperplane that separates the data points of one category from those of another in the most optimal way. But what does "optimal" mean in this context?
Optimality refers to the idea that the hyperplane should not only separate the two categories but should do so in a way that maximizes the margin between the closest points of each category and the hyperplane itself. Think of it not just as drawing a line in our field of flowers but as drawing the widest possible road that still keeps the daisies and roses on opposite sides. The edges of this road are marked by the nearest points (or "support vectors") of each category to the hyperplane, and the SVM algorithm seeks to make this road as wide as possible.
Why maximize the Margin?
The rationale behind maximizing the margin might seem counterintuitive at first glance. Here’s the reasoning: a hyperplane that has a large margin is likely to be more robust to noise and errors in new data. It's not just about the data we currently have but also about accurately predicting the classification of new, unseen data points. A wider road (or larger margin) means that small changes or uncertainties in the data are less likely to cause a misclassification.

Écrire commentaire