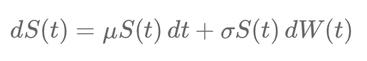
Think of the stochastic differential equation (SDE) as a formula that describes how stock prices change over time. It accounts for two key components: the predictable trends (deterministic part) and the random fluctuations (stochastic part). Together, these elements mimic real-world price movements, enabling investors and researchers to better understand and predict stock behavior.
SDEs in Financial Modeling
The value of an option is intrinsically tied to the price movement of the underlying stock. Since stock prices are influenced by both predictable trends and unpredictable fluctuations, option pricing models must incorporate both aspects. The SDE serves as the foundation for such models.
For example, the Black-Scholes-Merton model uses an SDE to simulate various potential paths of the underlying stock price. By analyzing these different paths, the model estimates the probability distribution of possible future stock prices, which is essential for accurate option valuation.
The general form of the SDE for stock prices is:
\[ dS(t) = \mu S(t) \, dt + \sigma S(t) \, dW(t) \]
Here:
- \( S(t) \): Stock price at time \( t \).
- \( \mu \): Drift, representing the expected return or trend of the stock.
- \( \sigma \): Volatility, representing the randomness or uncertainty in price movements.
- \( W(t) \): Standard Brownian motion, capturing the stochastic component.
By solving this equation, we obtain the Geometric Brownian Motion (GBM), a mathematical representation of stock prices under the Black-Scholes model:
\[ S(t) = S(0) \exp \left( \left(\mu - \frac{\sigma^2}{2}\right)t + \sigma W(t) \right) \]
Implied Volatility and the SDE
Implied volatility reflects the market's expectation of how much a stock's price might vary in the future. It is a crucial input for option pricing models. Through the SDE, we can understand how changes in implied volatility affect option prices.
For instance, higher implied volatility increases the range of possible future stock prices, impacting both the likelihood and magnitude of potential payoffs from options.
Mathematical Differentiation: Capturing Rates of Change
Differentiation is a mathematical tool that helps us understand how one quantity changes with respect to another. Imagine a graph that shows how far a car has traveled over time. Differentiation lets you zoom in and determine the car's speed at any given moment.
In finance, differentiation plays a crucial role in understanding how variables like stock prices or interest rates change over time. For instance, the derivative of the stock price with respect to time gives the instantaneous rate of change, capturing trends and volatility.
\[ \frac{dS}{dt} \]
This concept is used extensively in risk management, where changes in asset prices or portfolio values need to be analyzed and managed continuously.
In essence, the stochastic differential equation is a mathematical framework that captures the mix of predictable trends and unpredictable fluctuations in stock prices. Similar to how weather predictions estimate future temperatures based on past patterns and randomness, the SDE helps estimate how a stock's price might evolve over time. This blend of determinism and randomness makes SDEs indispensable for financial modeling, enabling traders and analysts to make informed decisions about investment strategies and risk management.

Écrire commentaire