Taylor expansion and Itô's Lemma are essentials tools, each tailored to a different type of system: deterministic or stochastic. While Taylor expansion provides approximations for smooth, predictable systems, Itô's Lemma extends these ideas to accommodate randomness—a necessity in modeling financial markets.
Taylor Expansion in Deterministic Systems
The Taylor expansion approximates a function \( f(x) \) by expressing its value near a point \( x_0 \) using its derivatives. It captures how the function changes with small variations \( dx \).
\[ f(x + dx) = f(x) + f'(x) dx + \frac{1}{2} f''(x) (dx)^2 + \dots \]
For small \( dx \), higher-order terms \( (dx)^n \) (\( n \geq 2 \)) diminish rapidly. This makes the first-order approximation:
\[ f(x + dx) \approx f(x) + f'(x) dx \]
sufficient for most deterministic applications. In such systems, small changes behave predictably, and higher-order corrections are often negligible.
The Stochastic Nature of Financial Markets
Financial markets, however, are inherently stochastic, driven by randomness and uncertainty. Price movements often follow models like geometric Brownian motion, where the change \( dX \) has both deterministic \( \mu dt \) and random \( \sigma dW(t) \) components:
\[ dX = \mu dt + \sigma dW(t) \]
Here:
- \( \mu \): Drift (average change rate).
-
- \( \sigma \): Volatility.
-
- \( dW(t) \): Increment of a Wiener process (random noise).
-
In stochastic systems:
- \( dW(t) \) has a mean of zero but variance proportional to \( dt \).
-
- \(dW(t)^2\) scales as \( dt \), meaning second-order terms must be retained.
-
From Taylor to Itô: A Necessary Adjustment
Itô's Lemma modifies Taylor expansion for stochastic processes. For a function \( f(X, t) \), where \( X \) follows a stochastic differential equation, the change \( df \) is:
\[ df(X, t) = \frac{\partial f}{\partial t} dt + \frac{\partial f}{\partial X} dX + \frac{1}{2} \frac{\partial^2 f}{\partial X^2} (dX)^2 \]
Key Difference: In stochastic calculus:
- \( (dX)^2 \) is nonzero and proportional to \( dt \): \( (dX)^2 = \sigma^2 dt \).
-
- This term represents the quadratic variation, capturing the effect of randomness.
-
Applications of Taylor Expansion in Finance
1. Bond Pricing and Interest Rate Risk
Taylor expansion approximates changes in bond prices due to small changes in interest rates:
\[ \Delta P \approx -D \cdot P \cdot \Delta y + \frac{1}{2} C \cdot P \cdot (\Delta y)^2 \]
Applications of Itô's Lemma in Finance
1. Pricing Exotic Options
Exotic options, such as barrier options and Asian options, rely on Itô's Lemma to model their payoffs under stochastic processes. For example, in barrier options, the payoff depends on whether the price crosses a specific level. Using Itô's Lemma, we determine the probability of crossing and adjust pricing formulas accordingly.
2. Stochastic Volatility Models
Models like Heston's include stochastic volatility, where both the price and volatility follow stochastic processes. Itô's Lemma is applied to derive equations that govern option prices under such conditions, capturing the interaction between price and volatility dynamics.
3. Greeks for Exotic Options
In exotic options, Itô's Lemma is used to calculate Greeks like Delta, Gamma, and Vega, incorporating the non-linear effects of stochastic factors. These sensitivities help manage risks associated with complex products.
Key Takeaways
- Taylor Expansion approximates small changes in smooth, deterministic systems by ignoring higher-order terms.
-
- Itô's Lemma extends Taylor's idea to stochastic systems by retaining second-order terms, essential for capturing randomness.
-
- Itô's Lemma is critical in pricing exotic options, stochastic volatility models, and risk management through Greeks calculation.

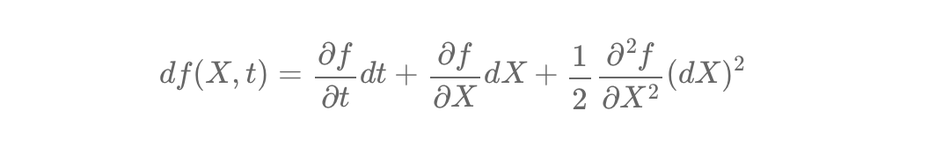
Écrire commentaire
Parth (mardi, 07 janvier 2025 19:46)
One of the best Explanations ✅�
Florian CAMPUZAN (mardi, 07 janvier 2025 20:16)
Thank you Parth.
Akash Umarbais (lundi, 13 janvier 2025 11:49)
This is a very clear explanation in simplest language. Thank you!!
Florian CAMPUZAN (lundi, 13 janvier 2025 11:58)
My pleasure Akash!