The Reflection Principle in Simple Terms

Imagine a serene lake with a mirror-like surface. Standing at a height of "a" units above the water, you drop a stone into the lake. The stone traces a path from your hand, descending toward the water. Upon making contact with the water's surface, the stone's reflection moves in the opposite direction beneath the water. This reflective path is the exact opposite of the stone's initial descent.

Consider a situation where the stone is 1 unit above the water. In this case, its reflection is 1 unit below. If the stone were 2 units above, its reflection would be 2 units below, and this pattern continues.

To determine the "height" of the reflected stone from the water's surface, you would use the formula:

\[ \text{Reflected Height} = 2a - (\text{height of the actual stone}) \]

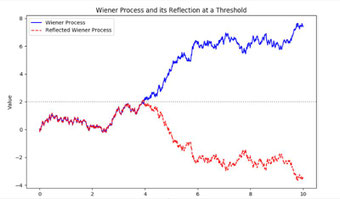
This analogy closely mirrors the principle seen in the Wiener process. When \( W_t \) surpasses a particular threshold \( a \) (much like the stone touching the water), its subsequent movements around \( a \) are reflected, forming a mirrored trajectory. For every time \( t > T \), the height of this mirrored process from the "surface" (level \( a \)) is calculated by:

\[ \text{Reflected Process} = 2a - W_t \]

Here, \( W_t \) represents the position of the particle (or the value of the process) at time \( t \).

The Reflection Principle

Now, regarding the reflection principle and the notion of a barrier at \( a \): If the Wiener process hits a level \( a \) at some time \( t \), it’s just as likely that, if there had been no barrier and the process had been free to move, it would’ve reached a level \( -a \) by that same time \( t \). This symmetry is the essence of the reflection principle.

Envision a particle experiencing Brownian motion, starting from \( W_0 = 0 \). This particle moves erratically. The main question is: What is the likelihood of this particle reaching a level \( a > 0 \) before time \( t \)? One approach is picturing a "barrier" at level \( a \). As the particle first collides with this barrier, think of it as spawning a mirrored counterpart that "reflects" back downward.

The beauty of this reflection concept is its grounding in the symmetry of Brownian motion: The chances of \( W_t \) being over level \( a \) equate to it being under level \( -a \).

Simplifying with the Reflection Principle

With the reflection principle in play, a complex question about the particle encountering a barrier morphs into a simpler query: When will two independent Brownian motions touch the level \( 0 \)? This switch greatly simplifies the math and associated calculations in numerous stochastic process problems.

Applications in Financial Options

The reflection principle becomes especially handy when studying barrier options, where the payoff depends on whether or not the underlying asset price reaches a certain level during the option's life. Consider an up-and-out call option: the option holder has the right to buy the underlying asset at a strike price \( K \), but the option is knocked out (becomes worthless) if the asset price exceeds a barrier \( B > K \).

By using the reflection principle, we can calculate the probability of the asset price hitting the barrier \( B \) before expiration. The principle simplifies the problem by relating the barrier crossing to a symmetric path in Brownian motion.

For example, the probability of an asset price reaching the barrier \( B \) before time \( t \), starting from an initial price \( S_0 \), can be expressed as:

\[ P(W_t > B) = 2P(W_t > B) - P(W_t < -B) \]

This calculation helps option pricing models accurately incorporate the likelihood of barriers being hit, affecting the fair value of barrier options.

Additionally, the reflection principle is invaluable for lookback options, where the payoff depends on the maximum or minimum price of the underlying asset during the option's life. By leveraging the reflection principle, traders can determine the joint distribution of the maximum \( W_s \) and the final price \( W_t \), facilitating efficient pricing and hedging strategies.

In conclusion, the reflection principle is a powerful tool in stochastic processes and finance. By simplifying complex problems involving barriers, it provides valuable insights for pricing and managing exotic options like barrier and lookback options, making it an essential concept in quantitative finance.