The Put-Call Symmetry (PCS) Simply Explained

Put-Call Symmetry (PCS) is a financial principle that provides a relationship between the prices of European put and call options with different strike prices but connected through the forward price of the underlying asset.

In order for put-call symmetry (PCS) to hold, the following assumptions are necessary:

1. Frictionless Markets: There are no transaction costs, taxes, or restrictions on short selling, and securities can be divided into any fraction.

2. No Arbitrage: There are no opportunities to make a risk-free profit from discrepancies in the pricing of securities.

3. Zero Drift: The expected return on the underlying asset is equal to the risk-free rate.

4. Symmetry Condition: The returns of the underlying asset are symmetrically distributed, meaning that the price of the underlying asset has no skewness or bias in either direction.

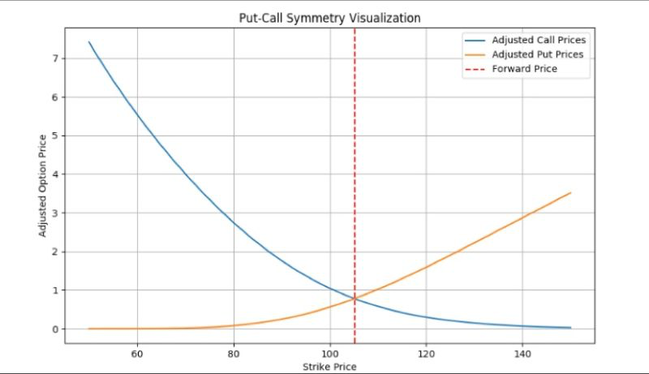
Under these conditions, PCS asserts that the adjusted prices of European calls and puts should be equal when their strikes are such that the geometric mean of the call strike (K) and the put strike (H) equals the forward price (F) of the underlying asset.

The forward price F is calculated by taking the current spot price S₀ and adjusting it for the risk-free rate r over time T:

\( F = S_0 \cdot e^{rT} \)

We set the strike prices for the call (K) and the put (H) so that their geometric mean equals the forward price:

\( \sqrt{K \cdot H} = F \)

Expanding this relationship further, we can square both sides to express it as:

\( K \cdot H = F^2 \)

This condition implies symmetry in the pricing of the options. We can generalize the payoff relationships by expressing the option prices based on their strike prices.

Symmetry Relationship Formula:

\( \frac{C(K)}{\sqrt{K}} = \frac{P(H)}{\sqrt{H}} \)

To further illustrate, suppose we substitute specific values:

Let \( K = 100 \), \( H = 121 \), and \( F = 110 \).

Calculating:

\( \sqrt{100 \cdot 121} = \sqrt{12100} = 110 \).

Therefore, the condition \( K \cdot H = F^2 \) is satisfied since:

\( 100 \cdot 121 = 110^2 \).

Practical Applications:

This formula can be used to evaluate relationships between options in markets with certain symmetry assumptions. For instance, a trader pricing a down-and-in put option can construct equivalent hedges using PCS relationships to approximate the exotic option's behavior.

Limitations:

Although PCS works well under theoretical assumptions, in practice, deviations due to bid-ask spreads, liquidity constraints, and other market imperfections may limit its direct applicability. Traders should complement PCS strategies with dynamic hedging when necessary.

PCS provides a mathematical foundation for pricing and hedging options symmetrically around the forward price. By leveraging its formulas, practitioners can simplify the analysis and replication of exotic payoffs. However, real-world conditions require adjustments to fully capture market complexities.