In the world of quantitative finance and stochastic calculus, certain multiplication rules are foundational in the modeling and analysis of random processes, such as the Brownian motion.
These rules, though succinct, encapsulate profound implications that enable the derivation of complex models integral to financial engineering, option pricing, and risk management.
The \( dW^2 = dt \) Rule
This rule originates from the quadratic variation of Brownian motion. When we evaluate the square of the Brownian motion's increments over a brief time interval \( \Delta t \), it equals the time interval itself. We express this mathematically by considering a sum of the squares of increments of the Wiener process \( W_t \) over a partition of an interval:
\[ \sum \left( W_{t_{i+1}} - W_{t_i} \right)^2 \approx \sum \Delta t_i = \Delta t \]
As the partition becomes finer, this approximation turns into an equality in the limit, leading to the rule:
\[ dW^2 = dt \]
This mathematical behavior underscores the roughness of the Brownian motion’s path. This roughness means that there is no point where a tangent can be drawn, illustrating the motion’s non-differentiability at any given point in time.
The intuition is that Brownian motion is like a series of tiny random steps. The longer the motion has to “wander,” the more uncertain or spread out its position becomes. Since each step adds to the overall uncertainty independently, the variance grows proportionally to the amount of time that has passed, resulting in a variance that equals time.
The Zero Rules: \( dt^2 = 0 \) and \( dt \, dW = 0 \)
These rules stem from the infinitesimal nature of the terms involved. For:
\[ dt^2 = 0 \]
it’s understood as the second-order term that becomes infinitesimally small and is thus neglected in differential equations.
For:
\[ dt \, dW = 0 \]
the rationale lies in the nature of \( dW \), which represents an increment of Brownian motion over an infinitesimal time interval \( dt \). Since Brownian motion has a mean of zero and variance of \( dt \), the product of \( dt \) and \( dW \) tends to zero faster than \( dt \) itself as \( dt \) approaches 0.
The statement:
\[ dt \, dW = 0 \]
is a result of the mathematical properties of Brownian motion and the infinitesimal increments involved in stochastic calculus.
Brownian motion is characterized by its randomness, where each increment is random and independent of others. Its mean is zero, indicating that upward and downward movements are equally likely over an infinitesimal time increment.
The variance of the Brownian motion over an infinitesimal time interval \( dt \) is:
\[ Var(dW) = dt \]
It signifies the dispersion or spread of the possible values of the Brownian motion, and in this case, it scales linearly with time.
When you multiply the infinitesimal time increment \( dt \) by the infinitesimal increment of the Brownian motion \( dW \), you're multiplying two small quantities. Since \( dW \) has a mean of zero and is random, on average, the product:
\[ dt \, dW \]
becomes much smaller than the individual increments \( dt \) or \( dW \).

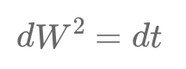
Écrire commentaire