The Kalman filter is a powerful algorithm widely used in quantitative finance to estimate a linear dynamic system's state from noisy measurements. It plays a crucial role in applications such as
asset tracking, portfolio management, and trend prediction.
The Kalman filter starts with an initial estimate of the system's true state and an associated uncertainty.
- Initial State Estimate (State): Our initial guess of the true value, e.g., a stock price.
- Initial Error Covariance Estimate (Error Covariance): Represents the initial estimate's uncertainty.
Two key matrices are involved in initialization:
- State Transition Matrix (A): Describes how the financial parameter changes over time.
- Observation Matrix (H): Maps the true state to observed measurements.
- Initial State Estimate (State): $100
- Initial Error Covariance Estimate (Error Covariance): $1 (Standard Deviation)
- Initial Estimate of Measurement Noise (Measurement Noise Covariance): $2 (Standard Deviation)
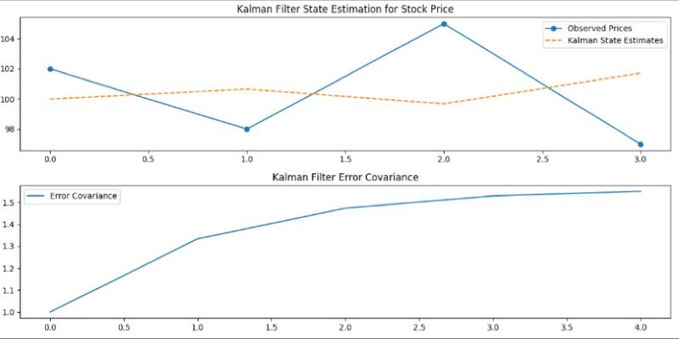
- Observed Price Data (with noise):
- Day 1: $102
- Day 2: $98
- Day 3: $105
- Day 4: $97
Time Step 1 (Day 1):
Prediction:
- Predicted State Estimate (Prior): $100 (no change)
- Predicted Error Covariance (Prior Covariance): $2 (process noise + measurement noise)
Update:
- Kalman Gain: 0.5 (Error Covariance / (Error Covariance + Measurement Noise Covariance))
- Corrected State Estimate (Posterior): $101 (Prior + Kalman Gain * (Observed Price - Prior))
- Corrected Error Covariance (Posterior Covariance): $1 (1 - Kalman Gain) * Prior Error Covariance
Time Step 2 (Day 2):
Prediction:
- Predicted State Estimate (Prior): $101 (previous Posterior)
- Predicted Error Covariance (Prior Covariance): $2 (process noise + measurement noise)
Update:
- Kalman Gain: 0.5 (Error Covariance / (Error Covariance + Measurement Noise Covariance))
- Corrected State Estimate (Posterior): $99.5 (Prior + Kalman Gain * (Observed Price - Prior))
- Corrected Error Covariance (Posterior Covariance): $1 (1 - Kalman Gain) * Prior Covariance
This process continues for each time step, optimally estimating the true state while considering uncertainty.
NOTA:
- Predicted Error Covariance: Estimated prediction uncertainty before new measurements.
- Corrected Error Covariance (Posterior): Updated prediction uncertainty after incorporating measurements.
- Corrected State Estimate (Posterior): Best estimate of the true state after considering prediction and measurements.
- Kalman Gain: Balances trust between measurements and predictions.

Write a comment