Indicator functions are crucial in financial mathematics, serving as binary conditions in the valuation of risky assets. They effectively act as switches in mathematical expressions, determining the inclusion or exclusion of certain terms based on the fulfillment of specific conditions.
For instance, when assessing the value of a zero-coupon bond in a risk-neutral environment (*), we consider the expected present value of the payoff, discounted at the risk-free rate. The formula
incorporates the indicator function to account for the possibility of issuer default. The valuation is expressed as:
E* [ exp(−∫ r(s) ds) * I{τ > T} ] from t to T
This formula assumes the payoff occurs only if the issuer does not default before the bond's maturity.
Building on this concept, let's consider a more complex scenario where we introduce the possibility of default before maturity. The value of a risky zero-coupon bond is then given by the sum of
two components – one reflecting the non-default scenario, and another accounting for the event of default. The formula for the valuation of a risky bond, considering the default risk,
is:
D(t,
T) = E* [ exp(-∫ from t to T of r(s) ds) * I{τ > T} + exp(-∫ from t to τ of r(s) ds) * δ * I{t < τ ≤ T} ]
Here, the first term under the expectation represents the value if no default occurs, while the second term adjusts the value for the possibility of default before maturity, weighted by the
recovery rate δ. This nuanced application of the indicator function allows financial analysts to model the complex dynamics of bonds where the risk of default is a significant
factor.
(*) A risk-neutral
environment assumes that there are no arbitrage opportunities, meaning that all assets are priced such that no risk-free profits can be made from market inefficiencies.
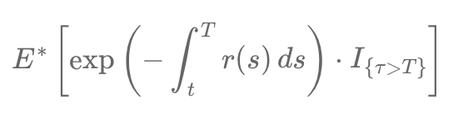
Écrire commentaire