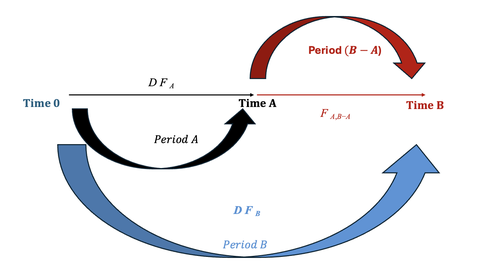
The forward pricing model ensures that an investor is indifferent between investing at the spot rate for a longer period or investing at the spot rate for a shorter period and reinvesting at the
forward rate. This condition is necessary to prevent arbitrage opportunities and ensure market efficiency.
The forward rate represents the implied return for an investment that will begin in the future. It is derived from spot rates and ensures that an investor earns the same
expected return whether they invest in a long-term bond today or roll over shorter-term investments at the forward rate.
Forward rates are denoted as \( f(A, B - A) \), which represents the forward rate agreed today for an investment that will start in \( A \) years and last for \( B - A \) years. For example, \(
f(1,2) \) is the rate agreed today for an investment that will begin in one year and last for two years.
Mathematical Expression of Indifference
The mathematical relationship that guarantees investment indifference is given by:
\[ (1 + z(n))^n = (1 + z(1)) \times (1 + f(1,1)) \times (1 + f(2,1)) \times ... \times (1 + f(n-1,1)) \]
where:
- \( z(n) \) is the spot rate for an investment of \( n \) years.
- \( f(m, k) \) is the forward rate agreed today for an investment starting in \( m \) years and lasting \( k \) years.
- \( n \) is the total maturity period.
This formula ensures that the future value of an investment is the same, whether an investor locks in the long-term spot rate today or reinvests periodically at forward rates.
Example: Computing Forward Rates
Consider today's Euro area yield spot rate curve:
- \( z(1) = 2.147507\% \) (1-year spot rate)
- \( z(2) = 2.074171\% \) (2-year spot rate)
- \( z(3) = 2.095010\% \) (3-year spot rate)
Step 1: Compute \( f(1,1) \) (1-year forward rate starting in year 1)
Using the formula:
\[ (1 + z(2))^2 = (1 + z(1)) \times (1 + f(1,1)) \]
Substituting values:
\[ (1.02074171)^2 = (1.02147507)^1 \times (1 + f(1,1)) \]
Solving for \( f(1,1) \):
\[ (1 + f(1,1)) = \frac{(1.02074171)^2}{(1.02147507)^1} \]
\[ f(1,1) = 2.00088\% \]
Step 2: Compute \( f(2,1) \) (1-year forward rate starting in year 2)
Using the formula:
\[ (1 + z(3))^3 = (1 + z(2))^2 \times (1 + f(2,1)) \]
Solving for \( f(2,1) \):
\[ (1 + f(2,1)) = \frac{(1.02095010)^3}{(1.02074171)^2} \]
\[ f(2,1) = 2.1367\% \]
Step 3: Compute \( f(1,2) \) (2-year forward rate starting in year 1)
Using the formula:
\[ (1 + z(3))^3 = (1 + z(1)) \times (1 + f(1,2))^2 \]
Solving for \( f(1,2) \):
\[ (1 + f(1,2))^2 = \frac{(1.02095010)^3}{(1.02147507)} \]
\[ f(1,2) = 2.06877\% \]
Why Should Investors Be Indifferent?
The forward pricing model ensures that investors receive the same expected return whether they invest at the long-term spot rate or at shorter-term
spot rates and reinvest at forward rates. If this relationship did not hold:
- Investors could borrow at a lower rate and reinvest at a higher forward rate, earning risk-free profits.
- Such arbitrage would distort market efficiency and misprice fixed-income securities.
By ensuring this balance, the market maintains fair pricing for bonds and interest rate products.
Notes
1. The forward rate \( f(1,1) \) represents the rate agreed today for an investment that will start in one year and last for one
year.

Écrire commentaire