The trigonometric circle naturally extends the concept of complex numbers, using the unit circle as a
framework to illustrate periodic phenomena. The binomial model in option pricing involves a financial
derivative's price evolving over time in a binomial tree, reflecting market uncertainty. By analyzing future payoffs' expected value under a risk-neutral measure, the problem can be expressed
using Fourier transforms. The characteristic function of the underlying asset's distribution is crucial, encoding key information about its behavior.
The link between binomial pricing models and Fourier transforms becomes even more apparent when we consider circular convolutions. Circular
convolution is a mathematical operation that combines two sequences by convolving them in a circular manner, where the end of one sequence wraps around to the beginning.
(*)
In a multi-period framework, the binomial tree approach can become time-consuming due to the exponential growth in the number of nodes as the number
of periods increases.
Instead of explicitly constructing and traversing the entire binomial tree, circular convolution allows us to compute the option prices at each time
step by convolving the option payoffs with the state price matrix. This convolution operation involves a fixed number of multiplications and additions, regardless of the number of periods.
Let's consider a simplified example where we have a two-period binomial option pricing model with a risk-neutral probability of 0.6 for an up move
and 0.4 for a down move. We'll visualize this scenario with the outer circle representing these probabilities and the inner circle containing different option payoffs.
Outer Circle (Adjusted Probabilities):
- Risk-neutral probability of 0.6 (up move) at 0 degrees.
- Risk-neutral probability of 0.4 (down move) at 180 degrees.
- Inner Circle (Option Payoffs):
We'll consider three different option payoffs represented at three different angles on the inner circle:
-
Option payoff of $100 at 0 degrees.
-
Option payoff of $150 at 90 degrees.
-
Option payoff of $200 at 180 degrees.
- Place the outer circle representing the risk-neutral probabilities with 0.6 at 0 degrees and 0.4 at 180 degrees.
- Place the inner circle representing the option payoffs with $100 at 0 degrees, $150 at 90 degrees, and $200 at 180 degrees.
- Rotate the inner circle clockwise by one position, corresponding to one time step. For example, the $200 payoff moves to 270 degrees. Perform circular convolution by multiplying each option payoff with the corresponding probability at the same angle on the outer circle and summing up the results.
Repeat this process for each time step.
(*) Convolution: from "convolvere", roll
together.
Inspiration from:
Introduction To Fast Fourier Transform In Finance ALES CERNY
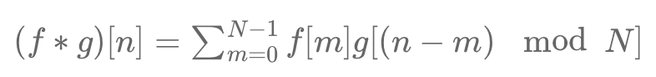
Écrire commentaire