Understanding correlation and tail dependence is essential in finance, as they describe different aspects of relationships between random variables. Correlation measures the linear relationship between two variables, while tail dependence focuses on extreme co-movements in the tails of their distributions. This distinction becomes particularly important in periods of financial stress, where extreme events dominate the dynamics.
Correlation is often quantified using the Pearson correlation coefficient, which ranges from -1 to 1. A value of 1 indicates a perfect positive linear relationship, -1 indicates a perfect
negative linear relationship, and 0 means no linear relationship. However, Pearson correlation only captures linear dependencies, meaning it fails to account for non-linear relationships or
dependencies during extreme events. This limitation makes it unsuitable for risk management applications where tail events drive outcomes.
Tail dependence provides a complementary perspective by describing the likelihood that two variables simultaneously take extreme values. It is quantified using the upper (λU) and lower (λL) tail dependence coefficients.
These coefficients measure how likely two variables are to exhibit extreme co-movements. Unlike correlation, which looks at average behavior, tail dependence focuses on rare, impactful events,
making it particularly relevant for stress testing and risk analysis.
Why Pearson Correlation is Linear
Pearson correlation is calculated as the covariance of two variables divided by the product of their standard deviations:
Here, \( \text{Cov}(X, Y) \) represents the covariance between \( X \) and \( Y \), and \( \sigma_X \) and \( \sigma_Y \) are their standard deviations. Covariance measures how two variables vary
together. If one variable is a linear function of the other, such as \( Y = aX + b \), the covariance is proportional to \( a \), making Pearson correlation a measure of linear proportionality.
However, for non-linear relationships, Pearson correlation often fails to capture the dependency, especially in the tails.
Link Between Affine Relationships and Linear Regression
An affine relationship (\( Y = aX + b \)) is the theoretical, deterministic link between two variables. The linear regression line, on the other hand, is the practical estimation of this relationship based on observed data. Pearson correlation measures how closely the data points align with this estimated linear regression line. If the correlation is high (\( \rho = 1 \) or \( -1 \)), the points lie almost perfectly along the regression line. If the correlation is low (\( \rho = 0 \)), the regression line may exist, but it has little predictive power.
An Example: CDO Tranches
Collateralized debt obligations (CDOs) are structured products divided into tranches of varying credit risk. Senior tranches are less exposed to risk, while junior (or equity) tranches absorb losses first. Under normal market conditions, the losses in senior and junior tranches might appear uncorrelated, as the senior tranche only absorbs losses after the junior tranche is exhausted. However, in extreme market scenarios, losses can cascade through all tranches, revealing a strong dependency between them.
Gaussian Copulas in CDO Modeling
Before the 2008 financial crisis, Gaussian copulas were widely used to model the dependency between CDO tranches. While these copulas performed well under normal conditions, they underestimated tail dependence. By construction, Gaussian copulas impose weak or no dependence in the tails, underestimating the risk of simultaneous extreme losses across tranches. This led to an overestimation of diversification benefits and underpricing of risk in senior tranches.
During the crisis, systemic stress revealed the hidden tail dependence between tranches. For instance, senior tranches, rated as low-risk based on Gaussian copulas, suffered significant losses
because they shared a hidden dependency with junior tranches during extreme scenarios. While the Pearson correlation between tranche losses might have seemed low under normal conditions, the
upper tail dependence coefficient highlighted their vulnerability in times of crisis.
This failure underscored the limitations of Gaussian copulas and the need for better tools, such as t-copulas or advanced stress-testing frameworks, that accurately capture tail dependence.
Ignoring tail dependence leads to severe underestimation of risk, as demonstrated by the mismanagement of CDOs prior to 2008.
Considering tail dependence alongside correlation is essential for robust risk assessments, particularly during crises. By leveraging advanced models, financial systems can better capture extreme
co-movements and enhance resilience.
Note
1. \( q \) represents the quantile level, which determines the threshold for extreme values. For example, when \( q = 0.95 \), \( F_X^{-1}(q) \) corresponds to the 95th percentile of \( X \), meaning the value below which 95% of observations lie. As \( q \) approaches 1 (or 0 for the lower tail), we focus on increasingly rare and extreme events.

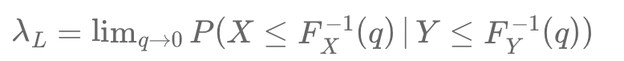
Écrire commentaire