The Correlation in CDO Tranches Simply Explained

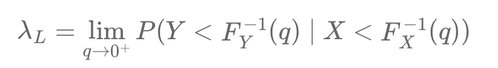
The assessment of risk in CDOs hinges on two pivotal concepts: probability theory and correlation among underlying assets. While probability theory offers insights into the likelihood of individual default events, correlation provides a measure of how these defaults are linked.

CDOs, structured into senior¹, mezzanine, and equity tranches , each bear varying degrees of risk based on their priority in loss absorption. The risk is inherently tied to the default probabilities of the underlying assets, such as loans or bonds. In this context, the relative frequency of defaults under different correlation scenarios becomes a focal point of risk assessment.

According to probability theory , the chance of two independent events occurring together is less than the chance of each occurring separately. In a mathematical context, if \( P(A) \) is the probability of event A and \( P(B) \) is the probability of event B, then the probability of both occurring simultaneously, assuming independence, is:

\[ P(A \cap B) = P(A) \cdot P(B) \]

This principle is critical for understanding the distribution of risks in CDOs. For instance, if the probability of event A happening is 0.2 and the probability of event B happening is 0.3, then the probability of both A and B happening together would be:

\[ P(A \cap B) = 0.2 \cdot 0.3 = 0.06 \]

This probability (0.06) is indeed less than the probability of either event occurring individually (0.2 and 0.3).

Correlation and its impact on risk between defaults of various assets in a CDO can significantly influence the overall risk profile. High correlation implies that defaults are likely to happen in tandem, potentially leading to large-scale simultaneous losses. On the other hand, low correlation suggests that defaults occur more independently.

Low correlation settings imply that the defaults of individual assets are largely independent. While the individual risk of default remains unchanged, the likelihood of multiple assets defaulting at the same time is comparatively lower. This leads to a higher relative frequency of smaller loss events, mostly impacting the equity or junior tranche. In such scenarios, the senior tranches are shielded from immediate losses due to the dispersion of risk among many independent defaults.

High correlation scenarios would mean a lower relative frequency of defaults but with potentially higher severity. Here, simultaneous defaults can erode the buffers of subordinated tranches quickly, exposing even the senior tranches to significant risk.

\[ \rho = \frac{Cov(X, Y)}{\sigma_X \cdot \sigma_Y} \]

While linear correlation, as expressed above, provides insights into average co-movement, it often fails to capture tail dependence , which plays a critical role in extreme market scenarios. Tail dependence measures the probability that extreme losses occur simultaneously and is particularly relevant for assessing systemic risk in CDOs.

\[ \lambda_L = \lim_{q \to 0^+} P(Y < F_Y^{-1}(q) \mid X < F_X^{-1}(q)) \]

This formula defines the lower tail dependence coefficient, quantifying the likelihood of joint extreme events in the lower tails of distributions.

Importance of tail dependence cannot be overstated in credit risk modeling, as defaults often cluster during crises, magnifying losses. Unlike correlation, tail dependence explicitly accounts for these co-movements in extreme scenarios, offering a more robust framework for evaluating CDO risk.

Practical Implications : Models based solely on correlation can underestimate systemic risk when defaults exhibit strong tail dependence. For example, Gaussian copulas, which assume no tail dependence, may fail to capture contagion effects observed during financial crises, leading to underpricing of risk in senior tranches.

Addressing this limitation requires incorporating copulas like the Clayton copula, which models asymmetric tail dependence and provides a more realistic representation of default clustering.

\[ C(u, v; \theta) = (u^{-\theta} + v^{-\theta} - 1)^{-1/\theta}, \quad \theta > 0 \]

Recognizing the limitations of linear correlation and emphasizing tail dependence enables analysts to develop models that better reflect real-world risks, improving pricing accuracy and portfolio resilience.

Notes:

¹ Drawing a parallel with societal norms where we prioritize protecting our seniors, in CDO structures, “senior” tranches are similarly safeguarded, being less subordinated and thus less exposed to initial losses.