A swap is priced by finding the "par swap rate," which is the fixed rate that makes the present value (PV) of all expected future floating cash flows equal to the PV of all future fixed cash flows. This ensures that the swap has a value of zero at the start.
Swap value = Value of the fixed-rate bond (VP) - Value of the floating-rate bond (VFL)
- Receive Fixed: This means buying the fixed-rate bond (VP).
- Pay Floating: This means shorting the floating-rate bond (VFL).
Floating and Fixed Value (VFL and VP):
VFL: It equals 1, as at each coupon payment date, the floating rate is reset, and the bond value returns to its par value.
VP: The value of the fixed-rate bond is calculated as:
VP = (C / (1 + t1)) + (C / (1 + t2)^2) + ... + (C / (1 + tn)^n) + (P / (1 + tn)^n), where:
C is the coupon rate for the fixed-rate bond.
P is the principal or face value (typically 1).
t1, t2, ..., tn are discount factors based on the spot rates for each period.
The discount factor (DF) for each period is given by:
1 / (1 + ti)^i
Solving for the Coupon Rate (C) :
The coupon rate C is found such that the bond is priced at par value (1) and is redeemed at par at maturity (P = 1). (*)
Final Equation:
The formula to solve for C is: C = (1 - DFn) / (DF1 + DF2 + ... + DFn)
Here, DFn is the discount factor for the last period n.
Example:
- Swap Term: 3 years
- Fixed Coupon Payments: Annually
- Spot Rates (used to calculate discount factors):
- Year 1: 5%
- Year 2: 5.5%
- Year 3: 6%
We want to calculate the fixed coupon rate (C) that makes the swap have zero value at inception.
Step-by-Step Calculation:
1. Calculate Discount Factors (DF) for each year based on the spot rates:
- DF1 = 1 / (1 + 0.05) = 0.9524
- DF2 = 1 / (1 + 0.055)^2 = 0.8984
- DF3 = 1 / (1 + 0.06)^3 = 0.8396
2. Calculate the value of the floating-rate bond (VFL):
Since the floating rate is reset to the market rate at each payment date, VFL = 1 (as explained earlier).
3. Calculate the value of the fixed-rate bond (VP):
VP = (C / (1 + t1)) + (C / (1 + t2)^2) + (C / (1 + t3)^3) + (1 / (1 + t3)^3)
Plugging in our discount factors:
VP = (C * 0.9524) + (C * 0.8984) + (C * 0.8396) + (1 * 0.8396)
4. Set VP equal to VFL (which is 1):
(
C * 0.9524) + (C * 0.8984) + (C * 0.8396) + (1 * 0.8396) = 1
5. Solve for C (fixed coupon rate):
Combine the terms involving C:
C * (0.9524 + 0.8984 + 0.8396) + 0.8396 = 1
Sum the discount factors:
C * (2.6900) + 0.8396 = 1
Subtract 0.8396 from both sides:
C * 2.6990 = 1 - 0.8396
C * 2.6990 = 0.1604
Solve for C:
C = 0.1604 / 2.6904
C ≈ 0.0596
So, the fixed coupon rate (C) that makes the swap have zero value at inception is approximately 5.94% per annum.
In this example, for a swap with a 3-year term and given spot rates, the fixed rate you would receive to offset the floating payments would be around 5.96%. This ensures the swap has zero value at inception, as the present value of fixed and floating cash flows are equal.
(*) The approach only works if the discount curve equals the forward curve because it assumes that the floating leg of the swap always resets to a value of 1, which holds true under this condition. If the curves differ, the floating leg's value will deviate from 1, and the method will no longer provide accurate results.
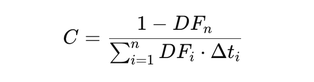
Écrire commentaire