“Pricer” un swap de taux vanille consiste à trouver le "taux de swap," soit le taux fixe qui rend la valeur actuelle (VA) de tous les flux de trésorerie flottants futurs égale à la VA de tous les flux de trésorerie fixes futurs. Cela garantit que le swap a une valeur nulle à son initiation, selon le principe d’absence d’opportunité d’arbitrage (AOA), qui prévient toute inégalité entre les parties au contrat.
Formule de Valeur d’un Swap
La valeur d’un swap peut s’exprimer comme suit :
\[ \text{Valeur du Swap} = \text{VA de la jambe fixe (VP)} - \text{VA de la jambe flottante (VFL)} \]
Analogies essentielles :
- Recevoir le taux fixe revient à investir dans une obligation à taux fixe (\( VP \)), c’est-à-dire être prêteur.
- Payer le taux variable revient à émettre une obligation à taux variable (\( VFL \)), c’est-à-dire être emprunteur.
Valeur de la Jambe Flottante (VFL)
La jambe flottante a une valeur toujours égale à 1, car à chaque date de réinitialisation, le taux variable est ajusté au marché, maintenant ainsi la valeur nominale.
Valeur de la Jambe Fixe (VP)
La VA de la jambe fixe est calculée comme suit :
\[ \text{VP} = \frac{C}{(1 + t_1)} + \frac{C}{(1 + t_2)^2} + \dots + \frac{C}{(1 + t_n)^n} + \frac{P}{(1 + t_n)^n} \]
où :
- \( C \): Le taux de coupon fixe.
- \( P \): Principal ou valeur nominale (généralement 1).
- \( t_1, t_2, \dots, t_n \): Facteurs d’actualisation pour chaque période.
Le facteur d’actualisation (\( DF \)) pour chaque période est donné par :
\[ DF_i = \frac{1}{(1 + t_i)^i} \]
Détermination du Taux Fixe (\( C \))
Le taux fixe \( C \) est déterminé de manière à ce que la VA de la jambe fixe soit égale à celle de la jambe flottante (1 à l’initiation). La formule pour \( C \) est :
\[ C = \frac{1 - DF_n}{DF_1 + DF_2 + \dots + DF_n} \]
Ici, \( DF_n \) est le facteur d’actualisation pour la dernière période.
Exemple : Calcul du Taux Fixe (\( C \))
Durée du swap : 3 ans. Coupons fixes payés annuellement. Taux spot utilisés :
- Année 1 : 5%
- Année 2 : 5,5%
- Année 3 : 6%
Étapes de calcul :
- Calculer les facteurs d’actualisation :
\[ DF_1 = \frac{1}{1 + 0.05} = 0.9524, \quad DF_2 = \frac{1}{(1 + 0.055)^2} = 0.8984, \quad DF_3 = \frac{1}{(1 + 0.06)^3} = 0.8396 \]
- Calculer \( VP \) :
\[ VP = (C \cdot 0.9524) + (C \cdot 0.8984) + (C \cdot 0.8396) + (1 \cdot 0.8396) \]
- Poser \( VP = VFL = 1 \) :
\[ (C \cdot 0.9524) + (C \cdot 0.8984) + (C \cdot 0.8396) + 0.8396 = 1 \]
- Résoudre \( C \) :
\[ C \cdot (0.9524 + 0.8984 + 0.8396) + 0.8396 = 1 \implies C \cdot 2.6904 = 0.1604 \implies C = \frac{0.1604}{2.6904} \approx 0.0596 \]
Le taux fixe (\( C \)) d’un swap de 3 ans est d’environ 5,96 %. Ce taux garantit que la valeur initiale du swap est nulle en équilibrant les VA des jambes fixe et flottante. Cet exemple illustre le principe d’absence d’arbitrage au cœur de la valorisation des swaps.
🎓 Formation recommandée : Les fondamentaux du risque et dérivés de taux
Comprenez les enjeux du risque de taux et apprenez à utiliser les instruments dérivés pour optimiser la gestion des expositions aux fluctuations des taux d’intérêt. Cette formation vous permettra de maîtriser les mécanismes des swaps de taux, options sur taux, futures et autres produits financiers utilisés à des fins de couverture.
Découvrir la formation🎓 Formation recommandée : Les fondamentaux de la Finance Quantitative
Découvrez les concepts essentiels de la finance quantitative, explorez les modèles mathématiques appliqués et apprenez à les utiliser pour la gestion des risques et la valorisation des actifs.
Découvrir la formation

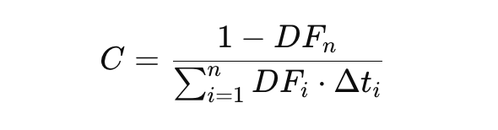
Écrire commentaire