Le pricing des options est une problématique centrale en finance, et la transformée de Fourier répond à la complexité de cet instrument financier.
Une option est un contrat financier qui donne à son détenteur le droit (mais non l'obligation) d'acheter ou de vendre un actif à un prix d’exercice spécifié, K, avant une certaine date d'expiration, T. Une option d'achat européenne, par exemple, permet à l'acheteur d'acquérir l'actif sous-jacent à K à la date T soit à l’échéance contrairement à l’option dite américaine exerçable à tout moment avant son échéance.
La problématique consiste à trouver la valeur actuelle de l'option, qui dépend du gain attendu à l'échéance. Le gain d’une option d’achat européenne est max(S_T - K, 0), où S_T est le prix de l'actif à la date T. Le prix actuel de l'option est donné par :
C = exp(-rT) E^Q[max(S_T - K, 0)]
où r est le taux d'intérêt sans risque, et E^Q désigne l'espérance sous la mesure neutre au risque.
Comme les prix futurs des actifs, S_T, suivent des processus stochastiques (par exemple, le modèle de Black-Scholes où les rendements suivent une distribution log-normale), il est difficile de prédire la distribution exacte et le gain attendu.
Des modèles plus complexes peuvent inclure des sauts et une volatilité stochastique. De plus, la fonction de gain max(S_T - K, 0) n'est pas différentiable en S_T = K, ce qui complique l'utilisation des méthodes différentielles traditionnelles. Par conséquent, des approches alternatives comme la transformée de Fourier sont nécessaires.
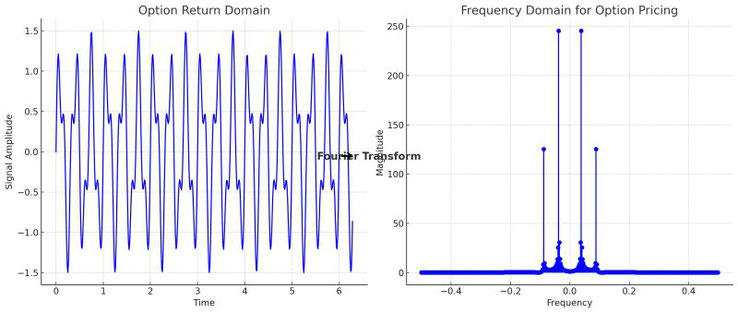
La transformée de Fourier est un outil mathématique qui décompose une fonction en une somme de sinusoïdes de différentes fréquences. Dans ce contexte, elle traduit une fonction du domaine temporel vers le domaine fréquentiel. Plus précisément, la transformée d'une fonction f(t) est donnée par :
F(ξ) = ∫ f(t) e^(-2iπξt) dt
où ξ (la lettre grecque "xi") représente la fréquence. En finance, f(t) correspond souvent à une distribution de rendements, et la transformée de Fourier révèle comment différentes fréquences contribuent à cette distribution.
L'idée principale est d'utiliser la transformée de Fourier pour convertir le calcul du gain attendu, complexe dans le domaine temporel, en un calcul plus simple dans le domaine fréquentiel. Cette transformation aide à gérer la discontinuité du gain et la complexité de la distribution des rendements.
La fonction caractéristique est essentielle dans ce processus. C'est essentiellement la transformée de Fourier de la distribution de probabilité des rendements, définie par :
φ(u) = E^Q[exp(iuX_T)]
où u est la fréquence et X_T = log(S_T) est le rendement logarithmique.
La fonction caractéristique encode toutes les informations sur S_T dans le domaine fréquentiel, représentant les rendements comme des combinaisons de sinusoïdes.
Une méthode bien connue qui utilise cette approche est la méthode de Carr-Madan sur laquelle je reviendrai dans un autre article de Blog très prochainement.

Écrire commentaire