Décomposition du terme d₁ dans la formule de Black-Scholes
Le terme \( d_1 \) dans la formule de Black-Scholes est crucial car il englobe plusieurs aspects de l'environnement de tarification des options. Décomposons-le :
\[ d_1 = \frac{\ln(S/K) + (r + \sigma^2/2)T}{\sigma \sqrt{T}} \]
Où :
- \( S \) : Prix actuel de l'action
- \( K \) : Prix d'exercice de l'option
- \( T \) : Temps jusqu'à l'expiration (en années)
- \( r \) : Taux d'intérêt sans risque (annualisé)
- \( \sigma \) : Volatilité de l'action (annualisée)
Décomposition de \( d_1 \) :
1. Logarithme naturel du ratio Stock/Strike : \( \ln(S/K) \)
Ce terme capture la position relative du prix de l'action par rapport au prix d'exercice. Si le prix de l'action est supérieur au prix d'exercice (\( S > K \)), ce terme est positif, indiquant une option dans la monnaie (in-the-money). Inversement, si le prix de l'action est inférieur au prix d'exercice (\( S < K \)), le terme est négatif, représentant une option hors de la monnaie (out-of-the-money). Le logarithme naturel transforme le ratio en une représentation de rendement composé de manière continue.
2. Compensation par le taux sans risque : \( rT \)
Ce terme représente la valeur temporelle de l'argent. Le taux sans risque est le rendement attendu d'un investissement entièrement sans risque sur la période \( T \). Ce terme ajuste la valeur de l'option pour tenir compte du fait que de l'argent aujourd'hui a plus de valeur que le même montant dans le futur en raison du coût d'opportunité du capital.
3. Ajustement de la volatilité : \( (\sigma^2/2)T \)
Ce terme compense la volatilité de l'action, qui mesure sa variabilité de prix. Les actions plus volatiles sont intrinsèquement plus risquées. Le terme \( \sigma^2 \times T \) compense ce risque supplémentaire. Le facteur \( 1/2 \) provient de l'équation différentielle stochastique qui régit l'évolution du prix de l'action (le mouvement brownien géométrique).
4. Dénominateur : Volatilité de l'action ajustée pour le temps : \( \sigma \sqrt{T} \)
Le dénominateur standardise le terme en fonction de la volatilité de l'action et de la racine carrée du temps jusqu'à l'expiration. À mesure que le temps jusqu'à l'expiration augmente, l'incertitude (ou la sensibilité de l'option à la volatilité de l'action) augmente également. Ce terme capture cette sensibilité. La racine carrée du temps est une conséquence du processus de diffusion qui sous-tend les mouvements de prix de l'action.
En résumé
\( d_1 \) peut être interprété comme la distance standardisée (en termes de volatilité) entre le prix actuel de l'action et le prix d'exercice, ajustée pour la valeur temporelle de l'argent et la variabilité future attendue du prix de l'action. C'est un terme complet qui saisit de nombreux aspects de la configuration de l'option et de l'environnement dans lequel elle existe.

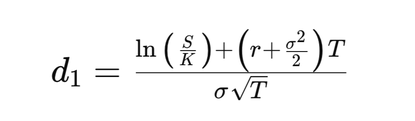
Écrire commentaire