Si vous considérez un processus de Wiener \(W_t\), et le multipliez par son intégrale \(\int_0^t W_s ds\), vous obtenez un produit de deux processus stochastiques : \[ W_t \cdot \int_0^t W_s ds. \]
Le produit et le calcul stochastique
Le produit \(W_t \cdot \int_0^t W_s ds\) est une fonction non linéaire du processus de Wiener. En calcul stochastique, traiter des fonctions non linéaires de processus stochastiques nécessite généralement des outils comme le lemme d'Itô, qui permet la différenciation et l'intégration de telles fonctions.
Le produit \(W_t \cdot \int_0^t W_s ds\) est lui-même un processus stochastique et hérite du caractère aléatoire du processus de Wiener. Son comportement est plus complexe que celui de \(W_t\) ou de \(\int_0^t W_s ds\) seul, en raison de l'interaction entre la valeur instantanée de \(W_t\) et ses valeurs accumulées passées.
Covariation quadratique
Ce produit est également lié au concept de covariation quadratique, qui est une mesure de la manière dont deux processus stochastiques co-varient dans un sens quadratique.
Dans le cas de \(W_t\) et de son intégrale, analyser leur covariation quadratique permet d’en appréhender leur comportement conjoint.
En effet, la covariation quadratique aide à comprendre l'interaction entre le processus de Wiener à un moment donné et son effet cumulé au fil du temps, de manière plus fine que la simple covariation linéaire.
Propriétés du processus de Wiener
Le processus de Wiener, également connu sous le nom de mouvement brownien, est souvent décrit comme "sans mémoire" car ses incréments sont indépendants. Cela signifie que le comportement futur du processus dépend uniquement de son état actuel et non de son historique.
Formellement, pour tout \(s < t\), l'incrément \(W_t - W_s\) est indépendant de l'historique du processus jusqu'au temps \(s\).
Interaction entre état actuel et historique
Cependant, l'intégrale \(\int_0^t W_s ds\) est une mesure cumulative. Elle additionne les valeurs du processus de Wiener dans le temps, intégrant ainsi l'historique du processus jusqu'au temps \(t\). Cette intégrale n'est pas sans mémoire car elle agrège des informations passées.
Multiplier \(W_t\) par son intégrale combine un processus sans mémoire à un moment spécifique dans le temps avec un processus cumulatif qui contient intrinsèquement des informations historiques.
Ce produit capture donc l’interaction entre l'état actuel, sans mémoire pris isolément, et l'effet agrégé de l'historique du processus qui lui ne l'est pas. Le produit \(W_t \cdot \int_0^t W_s ds\) peut être vu comme un reflet de la manière dont l'état actuel, sans mémoire à l'instant \(t\), subit l’influence du chemin cumulé qu'il a pris précédemment.
Application aux options exotiques
Cette interaction est particulièrement pertinente dans le cadre du pricing d’options exotiques, comme les options asiatiques dont le paiement dépend du chemin suivi avant l'instant \(t\).
🎓 Formation recommandée : Les fondamentaux de la Finance Quantitative
Découvrez les concepts essentiels de la finance quantitative, explorez les modèles mathématiques appliqués et apprenez à les utiliser pour la gestion des risques et la valorisation des actifs.
Découvrir la formation

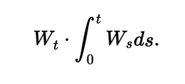
Écrire commentaire