Imaginez un lac serein avec une surface semblable à un miroir. Debout à une hauteur de « a » unités au-dessus de l'eau, vous laissez tomber une pierre dans le lac.La pierre trace un chemin de votre main, descendant vers l’eau. Lorsqu’elle entre en contact avec la surface de l’eau, le reflet de la pierre se déplace en sens inverse sous l’eau. Ce trajet réfléchi est exactement l’opposé de la descente initiale de la pierre.
Supposons que la pierre soit à 1 unité au-dessus de l’eau. Dans ce cas, son reflet est à 1 unité en dessous. Si la pierre se trouve à 2 unités au-dessus, son reflet sera à 2 unités en dessous, et ce schéma continue.
Pour déterminer la « hauteur » de la pierre réfléchie par rapport à la surface de l’eau, vous utiliseriez la formule : (2a - hauteur de la pierre réelle).
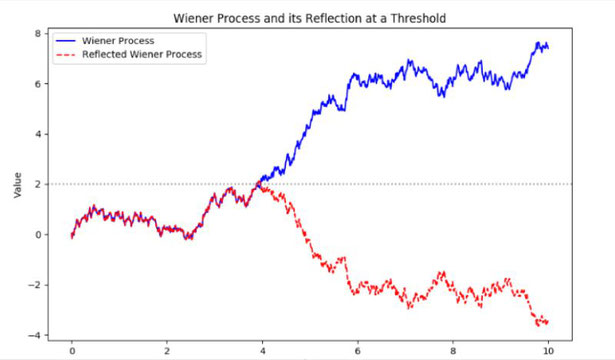
Cette analogie reflète de près le principe observé dans le processus de Wiener. Lorsque W_t dépasse un certain seuil « a » (à l’image de la pierre touchant l’eau), ses mouvements ultérieurs autour de « a » sont réfléchis, formant une trajectoire en miroir. Pour chaque instant t > T, la hauteur de ce processus réfléchi à partir de la « surface » (niveau « a ») est calculée par 2a - W_t.
Où W_t représente la position de la particule (ou la valeur du processus) à l’instant (t).
Concernant le principe de réflexion et la notion de barrière en (a) : Si le processus de Wiener atteint un niveau (a) à un moment (t), il est tout aussi probable que, s'il n'y avait pas eu de barrière et que le processus avait été libre de se déplacer, il aurait atteint un niveau (-a) au même instant (t). Cette symétrie est l’essence du principe de réflexion.
Imaginez une particule en mouvement brownien, commençant à W_0 = 0. Cette particule se déplace de manière erratique. La question principale est de savoir quelle est la probabilité que cette particule atteigne un niveau a > 0 avant un temps donné t.
Une approche consiste à imaginer une « barrière » au niveau a. Lorsque la particule entre en collision pour la première fois avec cette barrière, pensez à cela comme si elle engendrait un double en miroir qui « réfléchit » vers le bas.
La beauté de ce concept de réflexion repose sur la symétrie du mouvement brownien : les chances que W_t soit au-dessus du niveau a équivalent à celles qu'il soit en dessous du niveau -a.
Avec le principe de réflexion, une question complexe sur le fait que la particule rencontre une barrière se transforme en une question plus simple : quand deux mouvements browniens indépendants toucheront-ils le niveau 0 ? Ce changement simplifie grandement les calculs mathématiques dans de nombreux problèmes de processus stochastiques.
Ce principe devient particulièrement utile lors de l’étude des options américaines, où le moment de l’exercice correspond à un temps d’arrêt. Couplé au temps d’arrêt, le principe de réflexion offre un moyen de déterminer la distribution conjointe de la valeur maximale de Ws entre 0 et t, et de Wt. Cet aperçu s’avère précieux pour la tarification d’options uniques telles que les options barrières et les options à lookback.

Écrire commentaire