Le Modèle de Vasicek, nommé d'après Oldřich Vašíček, est un cadre mathématique fondamental utilisé en finance pour décrire l'évolution des taux d'intérêt au fil du temps. Il s'agit d'une équation différentielle stochastique (EDS) appartenant à la famille des modèles en temps continu, utilisée spécifiquement pour la modélisation des taux d'intérêt.
Caractéristiques principales du modèle de Vasicek :
1. Réversion vers la moyenne : Comme de nombreux modèles de taux d'intérêt, le modèle de Vasicek suppose que les taux d'intérêt tendent à revenir à une moyenne ou un niveau d'équilibre à long terme au fil du temps. Cette caractéristique reflète le comportement des taux d'intérêt observé dans les marchés réels.
2. Volatilité : Le modèle intègre la volatilité, permettant aux taux d'intérêt de varier de manière stochastique. Cela prend en compte l'incertitude et les fluctuations fréquemment observées dans les données des taux d'intérêt.
3. Vitesse de réversion vers la moyenne : Le modèle de Vasicek inclut un paramètre qui détermine la vitesse à laquelle les taux d'intérêt reviennent à la moyenne. Une vitesse de réversion élevée implique une convergence plus rapide vers le taux d'équilibre.
Mathématiquement, le modèle de Vasicek est représenté par l'équation différentielle stochastique suivante :
\( dr(t) = \kappa(\theta - r(t)) dt + \sigma dW(t) \)
Où :
\( r(t) \) : le taux d'intérêt à court terme au temps \( t \).
\( \kappa \) : la vitesse de réversion vers la moyenne.
\( \theta \) : le taux moyen ou d'équilibre à long terme.
\( \sigma \) : le paramètre de volatilité.
\( dW(t) \) : un processus de Wiener, représentant l'aléatoire.
Le modèle de Vasicek est largement utilisé sur les marchés obligataires et pour le pricing des dérivés de taux d'intérêt. Il offre un moyen structuré de modéliser l'évolution stochastique des taux d'intérêt au fil du temps.
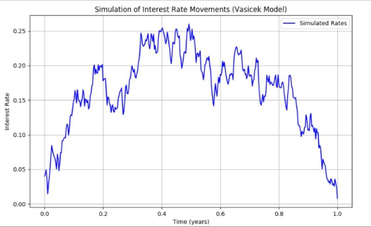
Exemple : Simulation des taux d'intérêt à l'aide du modèle de Vasicek
Données initiales :
Taux moyen à long terme (\( \theta \)) : 5 %
Vitesse de réversion (\( \kappa \)) : 0,1
Volatilité (\( \sigma \)) : 0,2
Taux initial (\( r(0) \)) : 4 %
Objectif : Simuler les taux d'intérêt sur une année avec des pas de temps quotidiens.
Étapes :
1. Définir le pas de temps (\( \Delta t \)) et le nombre de pas de temps (\( N \)) :
\( \Delta t = \frac{1}{365} \) (quotidien), \( N = 365 \) (une année).
2. Initialiser \( r(0) = 0,04 \) et créer un tableau pour stocker les taux simulés.
3. Simuler les variations de taux d'intérêt de manière itérative en utilisant le modèle de Vasicek :
\( r(t + \Delta t) = r(t) + \kappa(\theta - r(t)) \Delta t + \sigma \sqrt{\Delta t} Z \)
Ici, \( Z \) est une variable aléatoire tirée d'une distribution normale standard (\( Z \sim N(0, 1) \)).
4. Répéter cette étape pour tous les \( N = 365 \) pas de temps pour générer une trajectoire complète des taux d'intérêt.
Exemple détaillé :
Calculons les trois premiers jours avec des valeurs d'exemple pour \( Z \) :
- Jour 1 : Soit \( Z = 0,5 \).
\( r(1) = 0,04 + 0,1(0,05 - 0,04)(1/365) + 0,2 \sqrt{1/365} \cdot 0,5 \)
\( r(1) \approx 0,04 + 0,00000274 + 0,002612 \)
\( r(1) \approx 0,04261 \) (ou 4,261 %). -
- Jour 2 : Soit \( Z = -0,3 \).
\( r(2) = 0,04261 + 0,1(0,05 - 0,04261)(1/365) + 0,2 \sqrt{1/365} \cdot (-0,3) \)
\( r(2) \approx 0,04261 + 0,00000202 - 0,001566 \)
\( r(2) \approx 0,04105 \) (ou 4,105 %). -
- Jour 3 : Soit \( Z = 0,8 \).
\( r(3) = 0,04105 + 0,1(0,05 - 0,04105)(1/365) + 0,2 \sqrt{1/365} \cdot 0,8 \)
\( r(3) \approx 0,04105 + 0,00000245 + 0,004177 \)
\( r(3) \approx 0,04523 \) (ou 4,523 %).
Répétez ce processus pour tous les 365 jours avec de nouvelles valeurs aléatoires pour \( Z \) à chaque étape.
Résultats simulés :
Résultats simulés (exemple) :
Jour 1 : 4,261 %
Jour 2 : 4,105 %
Jour 3 : 4,523 %
...
Jour 365 : 4,982 %
Le modèle de Vasicek fournit un cadre puissant pour simuler des trajectoires réalistes des taux d'intérêt au fil du temps. En intégrant la réversion vers la moyenne, la volatilité et l'aléatoire, il modélise efficacement le comportement des taux d'intérêt sur les marchés financiers.

Écrire commentaire