Le modèle de Merton est reconnu comme une pierre angulaire des modèles structurels utilisés pour évaluer la probabilité de défaut dans l'analyse du risque de crédit. Son approche consistant à considérer les actions d'une entreprise comme une option d'achat sur ses actifs a ouvert la voie au développement et à l'amélioration des modèles structurels dans le secteur financier.
Selon ce modèle, la valeur des actifs d'une entreprise à tout moment t (At) est composée de ses capitaux propres (Et) et de sa dette à coupon zéro (Dt) avec une valeur nominale K, arrivant à maturité à un moment futur T, où T est supérieur à t. Cette relation forme l'équation At = Et + Dt. À la maturité de la dette (T), la valeur des capitaux propres (Et) est déterminée comme étant le maximum de At - K ou zéro. Si At dépasse K, les actionnaires bénéficient de la différence ; sinon, les capitaux propres deviennent sans valeur, ce qui conduit au défaut de paiement.
Le modèle de Merton utilise la formule de Black-Scholes pour valoriser cette « option d'achat » sur les actifs de l'entreprise, où :
E = At * N(d1) - K * e^(-r(T-t)) * N(d2).
où:
- E est la valeur des capitaux propres.
- N() est la fonction de répartition cumulée de la distribution normale standard, et d1 et d2 sont des fonctions de la valeur des actifs, du niveau de la dette, du taux d'intérêt sans risque r, et de la volatilité des actifs sigma.
Cependant, malgré le fait d’être un modèle structurel pionnier du risque de crédit, le modèle de Merton a été critiqué. Sa forte dépendance aux données de marché pour estimer la valeur des actifs et la volatilité limite son applicabilité aux entreprises privées ou à celles ayant des actions moins liquides.
Les hypothèses du modèle, notamment des marchés sans frictions et l’incapacité de l'entreprise à renégocier sa dette, ne sont pas toujours alignées avec les conditions réelles. Il a tendance à sous-estimer les risques de défaut à court terme et peut ne pas fournir de signes précurseurs de détresse financière.
Ces critiques ont encouragé le développement de modèles alternatifs, tels que les modèles de forme réduite. Ces modèles traitent le défaut comme un événement soudain et imprévisible, influencé par des facteurs externes, et utilisent souvent des méthodes stochastiques comme le processus de Poisson pour modéliser les défauts.
Contrairement aux modèles structurels, les modèles de forme réduite ne dépendent pas de la structure d'actifs et de passifs de l'entreprise et sont adaptables à un plus large éventail d’emprunteurs. Ils se sont avérés particulièrement utiles pour le pricing des dérivés de crédit tels que les Credit Default Swaps.
Bien que le modèle de Merton ait apporté une avancée majeure dans la modélisation du risque de crédit en appliquant la théorie de la valorisation des options aux capitaux propres d’une entreprise, ses limites ont conduit à l'émergence d'autres modèles, notamment les modèles de forme réduite. Ces nouveaux modèles surmontent certaines des faiblesses du modèle de Merton, en particulier dans les situations où les données de marché sont rares ou peu fiables, offrant des moyens alternatifs pour comprendre et quantifier le risque de crédit.

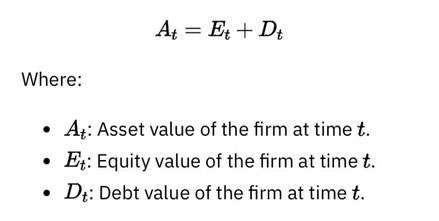
Écrire commentaire