Le calcul stochastique est une branche des mathématiques financières et des probabilités qui permet de modéliser et d’analyser des phénomènes aléatoires en continu, tels que les prix des actifs financiers. L’un des outils les plus importants de cette discipline est le calcul d’Itô, qui permet de différencier des fonctions de processus stochastiques, notamment celles qui dépendent d’un mouvement brownien. Ce calcul diffère sensiblement du calcul différentiel classique et nécessite une approche adaptée pour tenir compte des propriétés stochastiques.
Mouvement Brownien : Propriétés Clés
Le mouvement brownien, souvent noté \( W_t \), est un processus stochastique jouant un rôle central en finance et en probabilités. Ses propriétés fondamentales sont :
- \( W_0 = 0 \) : Le mouvement commence à l'origine.
- \( W_{t+s} - W_t \) est indépendant de l’histoire de \( W_t \) jusqu’à \( t \).
- \( W_{t+s} - W_t \sim \mathcal{N}(0, s) \) : Pour \( s > 0 \), les incréments suivent une loi normale de moyenne nulle et de variance \( s \).
- Les trajectoires de \( W_t \) sont continues mais non différentiables presque partout.
Ces propriétés font du mouvement brownien un modèle idéal pour décrire l’évolution des prix d’actifs, des taux d’intérêt ou d’autres phénomènes financiers ou physiques aléatoires.
Calcul Différentiel Classique vs. Calcul Stochastique
Lorsque l’on manipule des processus stochastiques comme \( W_t \), il est tentant d’essayer de les différencier de la même manière que les fonctions lisses dans le calcul classique. Cependant, cette approche échoue car \( W_t \) n’est pas différentiable dans le sens classique.
Considérons la fonction \( t \mapsto W_t^2 \). En calcul classique, on écrirait :
\[ \frac{d}{dt}[W_t^2] = 2 W_t \cdot \frac{dW_t}{dt}. \]
Cependant, comme \( W_t \) est un mouvement brownien, \( \frac{dW_t}{dt} \) n’existe pas dans le sens habituel. Une autre méthode est donc nécessaire—le calcul d’Itô intervient ici.
La Formule d’Itô
La formule d’Itô est l’analogue stochastique de la règle de différentiation classique. Pour une fonction \( g(t, W_t) \) régulière (deux fois continûment différentiable par rapport à \( W_t \) et une fois par rapport à \( t \)), la formule est :
\[ dg(t, W_t) = \frac{\partial g}{\partial t} dt + \frac{\partial g}{\partial W_t} dW_t + \frac{1}{2} \frac{\partial^2 g}{\partial W_t^2} (dW_t)^2. \]
Les termes se décomposent ainsi :
- Dérive : \( \frac{\partial g}{\partial t} dt \), correspondant à la dérivée classique par rapport au temps.
- Terme stochastique : \( \frac{\partial g}{\partial W_t} dW_t \), représentant la variation due au mouvement brownien.
- Covariation : \( \frac{1}{2} \frac{\partial^2 g}{\partial W_t^2} (dW_t)^2 \), un terme supplémentaire par rapport au calcul classique.
Dans le calcul d’Itô, \( (dW_t)^2 = dt \), reflétant la variance du mouvement brownien sur un intervalle de temps infinitésimal.
Exemple d’Application : \( W_t^2 \)
Pour illustrer, considérons \( g(t, W_t) = W_t^2 \). Appliquons la formule d’Itô étape par étape :
Étape 1 : Calcul des Dérivées Partielles
- \( \frac{\partial g}{\partial t} = 0 \) (pas de dépendance explicite en \( t \)).
- \( \frac{\partial g}{\partial W_t} = 2 W_t \).
- \( \frac{\partial^2 g}{\partial W_t^2} = 2 \).
Étape 2 : Appliquer la Formule d’Itô
\[ d(W_t^2) = 0 \cdot dt + 2 W_t \cdot dW_t + \frac{1}{2} \cdot 2 \cdot (dW_t)^2. \]
Étape 3 : Simplifier
\[ d(W_t^2) = 2 W_t \cdot dW_t + dt. \]
Intégration de la Formule d’Itô
En intégrant de \( 0 \) à \( t \), on obtient :
\[ W_t^2 = W_0^2 + 2 \int_0^t W_s \, dW_s + t. \]
Si \( W_0 = 0 \), cela simplifie en :
\[ W_t^2 = 2 \int_0^t W_s \, dW_s + t. \]
Contrairement au calcul classique, où les trajectoires sont lisses, celles du mouvement brownien oscillent rapidement et de manière imprévisible. La formule d’Itô prend en compte ces irrégularités via le terme de covariation \( \frac{1}{2} \frac{\partial^2 g}{\partial W_t^2} (dW_t)^2 \), qui, pour \( W_t^2 \), se traduit par le terme additionnel \( t \).

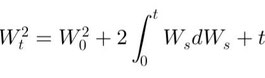
Écrire commentaire