Il est essentiel de comprendre le risque de défaillance simultanée de plusieurs entités, en particulier lorsqu'il s'agit de dérivés de crédit tels que les basket credit default swaps. La probabilité conjointe de défaut et sa corrélation sont des éléments clés pour comprendre ce risque.
La corrélation entre deux variables aléatoires X et Y est donnée par la formule :
corrélation(X, Y) = covariance(X, Y) / (σ_X * σ_Y)
Où :
-
covariance(X, Y) est la covariance entre X et Y.
- σ_X et σ_Y sont les écarts-types de X et Y, respectivement.
Pour les événements de défaut, on traite souvent des variables indicatrices 1_A et 1_B qui prennent la valeur 1 si le défaut se produit et 0 sinon. La covariance entre ces variables indicatrices peut être définie comme suit :
covariance(1_A, 1_B) = E[1_A * 1_B] - E[1_A] * E[1_B]
Ici :
E[1_A] = p(A) est la probabilité de défaut de l'entité A.
E[1_B] = p(B) est la probabilité de défaut de l'entité B.
E[1_A * 1_B] = p(A et B) est la probabilité conjointe de défaut de A et B.
Pour un événement de défaut A, où x_i peut être 0 ou 1 :
E[1_A] = 1 * p(A) + 0 * (1 - p(A)) = p(A)
La variance est l'espérance du carré de l'écart par rapport à la moyenne : Var(1_A) = E[(1_A - p(A))^2]
Comme (1_A) peut être 0 ou 1, on peut développer cette formule comme suit : Var(1_A) = p(A) * (1 - p(A))^2 + (1 - p(A)) * (0 - p(A))^2 [1]
En simplifiant, on obtient :
Var(1_A) = p(A) * (1 - p(A))^2 + (1 - p(A)) * p(A)^2 = Var(1_A) = p(A) * (1 - p(A))
En utilisant ces définitions, la corrélation de défaut peut être exprimée comme suit :
corr(A, B) = [p(A et B) - p(A) * p(B)] / √[(p(A) * (1 - p(A)) * p(B) * (1 - p(B))]
Et la probabilité conjointe de défaut : p(A et B) = corrélation(A, B) * √[(p(A) * (1 - p(A)) * p(B) * (1 - p(B))] + p(A) * p(B)
Considérons un investissement égal de 5 millions de dollars dans deux obligations (B1 et B2) avec les paramètres suivants :
-
Probabilité de défaut pour les deux obligations p(A) = p(B) = 0,05 (5 %).
-
Corrélation de défaut corr(A, B) = 0,3.
- Taux de recouvrement = 0.
La probabilité conjointe de défaut = 0,3 * √[(0,05 * 0,95) * (0,05 * 0,95)] + 0,05 * 0,05 = 0,1675
La perte attendue est p(A et B) = 0,1675 * 10 M = 167 500 $.
[1]
Lorsqu’on calcule la variance, “prendre l’espérance” signifie faire une moyenne pondérée des écarts au carré par rapport à la moyenne, selon les probabilités associées à chaque valeur possible. Ainsi, la variance mesure la dispersion des valeurs en tenant compte de leur probabilité de se produire.
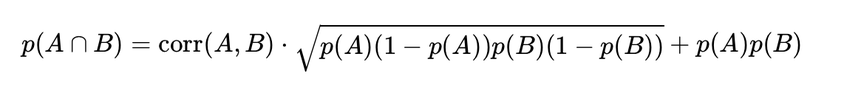
Écrire commentaire