La fonction de densité de probabilité (PDF) en termes simples

La Fonction de Densité de Probabilité (PDF) d’une variable indique la probabilité de trouver la variable à une valeur spécifique. Pour une distribution normale standard avec une moyenne de 0 et un écart-type de 1, la PDF est exprimée par :

 

φ(x) = 1 / (√(2 * π)) * e^(-x^2 / 2)

 

La valeur de φ(x) à n'importe quel point x donne la probabilité relative que la variable se situe près de ce point. Pour trouver la probabilité que la variable soit comprise entre deux points, on calcule l’aire sous la courbe de φ(x) entre ces deux points.

 

La Fonction de Répartition (CDF) fournit la probabilité que la variable soit inférieure ou égale à une valeur x. Pour la distribution normale standard, la CDF au point x est calculée en intégrant la PDF de moins l’infini jusqu’à x :

 

N(x) = ∫ de -∞ à x de φ(t) dt

 

La CDF augmente de 0 à 1 lorsque x se déplace de gauche à droite sur la droite numérique. À x=0, le point central de la courbe en cloche, N(0) est 0,5, ce qui indique qu’il y a 50 % de chances que la variable soit inférieure ou égale à zéro, en raison de la symétrie de la courbe.

 

En termes plus simples :

 

• φ(x) nous indique la densité de probabilité à un point particulier x.

• N(x) nous indique la probabilité que la variable soit inférieure ou égale à x.

 

Le lien entre la CDF et la PDF :

 

Les valeurs de la CDF N(d1) et N(d2) sont essentielles dans le modèle de Black-Scholes, qui aide à déterminer le prix théorique des options.

 

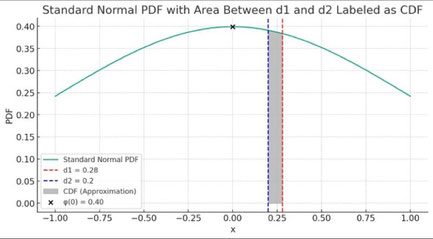
Lorsque l'on approxime la différence entre N(d1) et N(d2) pour des valeurs de d1 et d2 proches l'une de l'autre, on peut utiliser le fait que la PDF φ(x) est presque constante entre d1 et d2 s'ils sont proches du centre de la distribution (x = 0). 

Ainsi, on peut approximer la différence entre les CDFs, N(d1) - N(d2), comme l’aire sous la courbe PDF entre d1 et d2 :

 

• N(d1) - N(d2) ≈ φ(0) * (d1 - d2) (*)
  

 

En remplaçant la valeur de φ(0), on obtient :

 

• N(d1) - N(d2) ≈ (1 / (√(2 * π))) * (d1 - d2)= 1 / (√(2 * π) ≈ 0,4

 

Cette approximation est une manière pratique d’estimer la probabilité qu’une variable aléatoire normalement distribuée se situe entre d1 et d2, ce qui est un calcul fréquent dans les modèles financiers comme la formule de Black-Scholes pour la valorisation des options.

 

(*) Aire d’un rectangle = hauteur * largeur.