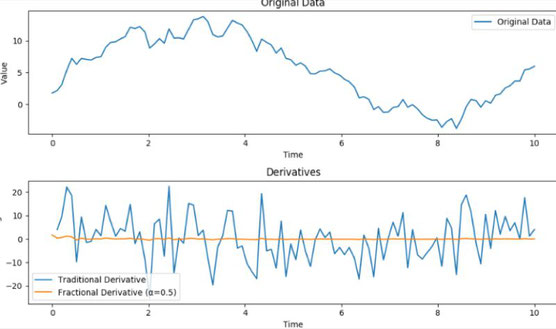
Imaginez que vous suivez quelque chose qui change au fil du temps, comme la température. La dérivation traditionnelle est comme vérifier la température actuelle, vous donnant le taux de changement à cet instant précis sans tenir compte des températures passées.
1. Dérivation traditionnelle (sans mémoire) : Lorsque vous calculez la première dérivée, c'est comme regarder la température à ce moment précis. Aucune mémoire, aucune considération des températures passées.
2. Dérivation fractionnaire (mémoire incluse) : La dérivation fractionnaire va au-delà du moment actuel. C'est comme demander : « Comment la température a-t-elle changé au cours de la dernière heure ou journée ? »
- La dérivation fractionnaire se souvient des changements passés. Elle prend en compte comment les températures passées influencent le taux de changement actuel.
- Par exemple, s'il a fait de plus en plus chaud au cours de la dernière heure, la dérivation fractionnaire reflète cette mémoire et prédit un taux de changement positif en raison de ces augmentations passées.
Voyons maintenant comment cela s'applique à la finance :
1. Modèles de prix des actifs : Les experts financiers (ici les quants) utilisent des modèles pour expliquer le comportement des prix des actifs au fil du temps. Les modèles traditionnels supposent que les variations de prix sont indépendantes, sans mémoire des mouvements passés. Mais les prix réels ont des effets mémoriels, comme l'autocorrélation et des schémas de volatilité.
- Mouvement brownien fractionnaire (fBm) : La dérivation fractionnaire introduit la mémoire dans les modèles. Le mouvement brownien fractionnaire, par exemple, tient compte de la dépendance à long terme, capturant les tendances persistantes et les schémas de volatilité dans les prix des actifs.
2. Modèles de gestion des risques : En gestion des risques, les modèles estiment les pertes potentielles. Les modèles de Value at Risk (VaR), par exemple, s'appuient sur les données historiques. La dérivation fractionnaire tient compte des effets mémoriels dans les données de marché, assurant que les modèles de risque reflètent précisément l'impact des conditions de marché passées sur le risque futur.
3. Modèles de valorisation d’options : La valorisation de dérivés financiers complexes nécessite de modéliser les mouvements des prix des actifs sous-jacents. Le calcul fractionnaire améliore ces modèles en incluant les effets mémoriels dans les simulations de prix.
4. Modèles de taux d'intérêt : La valorisation des obligations et la modélisation de la courbe des taux tiennent compte des données historiques de la courbe des taux. La dérivation fractionnaire capture la mémoire des changements de taux d'intérêt, améliorant la modélisation de la dynamique de la structure par terme.
En essence, la dérivation fractionnaire comble le fossé entre les observations actuelles et les influences passées, ce qui en fait un outil précieux en finance quantitative.

Écrire commentaire