Les algorithmes avancés permettent aux ordinateurs d'identifier des motifs, de prendre des décisions, et même de prédire l'avenir à partir de données. Parmi ces outils puissants, l’algorithme de la machine à vecteurs de support (SVM) se distingue par son efficacité, en particulier dans le domaine de la classification. Mais comment fonctionne-t-il ?
Démystifions cet algorithme en commençant par l'un de ses concepts fondamentaux : l'hyperplan.
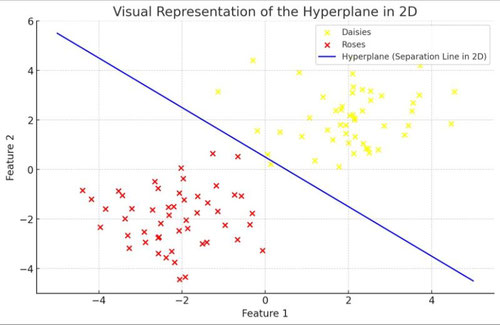
Imaginez que vous êtes dans un parc et que vous observez un grand champ ouvert avec différents types de fleurs éparpillées. Votre tâche est de tracer une ligne droite qui sépare deux types de fleurs, par exemple des marguerites et des roses, de sorte que toutes les marguerites soient d'un côté de la ligne et toutes les roses de l'autre. En deux dimensions, comme dans notre champ, cette ligne est similaire à ce que les mathématiciens appellent un "hyperplan".
Dans le contexte de la SVM, nous ne travaillons pas souvent avec des champs et des fleurs, mais plutôt avec des points de données dans des espaces pouvant avoir de nombreuses dimensions au-delà de deux. Si nous avions affaire à trois caractéristiques (comme la taille, la couleur et l'odeur des fleurs), nous serions dans un espace tridimensionnel, et notre "ligne" serait en fait une feuille plane qui divise l'espace en deux parties. Cette feuille plane est décrite mathématiquement comme (ax + by + cz + d = 0), où (a), (b), et (c) sont des coefficients qui définissent l'orientation du plan dans l'espace tridimensionnel, et (d) est le décalage par rapport à l'origine.
À mesure que nous augmentons les dimensions, notre hyperplan reste l'élément qui sépare proprement nos données en deux catégories, mais il devient plus difficile à visualiser.
L’hyperplan est au cœur de l’algorithme SVM. L’objectif de la SVM est de trouver le meilleur hyperplan qui sépare les points de données d’une catégorie de ceux d’une autre de manière optimale. Mais qu'entend-on par "optimal" dans ce contexte ?
L'optimalité signifie que l'hyperplan ne doit pas seulement séparer les deux catégories, mais doit le faire de manière à maximiser la marge entre les points les plus proches de chaque catégorie et l'hyperplan lui-même. Il ne s’agit pas seulement de tracer une ligne dans notre champ de fleurs, mais de tracer la route la plus large possible qui maintient les marguerites et les roses de part et d'autre. Les bords de cette route sont marqués par les points les plus proches (ou "vecteurs de support") de chaque catégorie par rapport à l’hyperplan, et l’algorithme SVM cherche à rendre cette route aussi large que possible.
Pourquoi maximiser la marge ?
La raison derrière la maximisation de la marge peut sembler contre-intuitive au premier abord. Voici l'explication : un hyperplan qui a une grande marge est probablement plus robuste au bruit et aux erreurs dans de nouvelles données. Il ne s’agit pas seulement des données que nous avons actuellement, mais aussi de prédire correctement la classification de nouveaux points de données non encore observés. Une route plus large (ou une marge plus grande) signifie que de petits changements ou incertitudes dans les données sont moins susceptibles de provoquer une mauvaise classification.

Écrire commentaire