Stochastic calculus is a branch of financial mathematics and probability that models and analyzes continuous random phenomena, such as asset prices. One of its key tools is Itô calculus, which allows differentiation of functions of stochastic processes, particularly those involving Brownian motion. This type of calculus differs significantly from classical differential calculus and requires a tailored approach to account for stochastic properties.
Brownian Motion: Key Properties
Brownian motion, often denoted as \( W_t \), plays a central role in finance and probability. Its defining properties are:
- \( W_0 = 0 \): The motion starts at the origin.
- \( W_{t+s} - W_t \) is independent of the history of \( W_t \) up to time \( t \).
- \( W_{t+s} - W_t \sim N(0, s) \): For any \( s > 0 \), the increments follow a normal distribution with zero mean and variance \( s \).
- The paths of \( W_t \) are continuous but almost nowhere differentiable.
These properties make Brownian motion an ideal model to describe the evolution of asset prices, interest rates, or other financial or physical random phenomena.
Classical Calculus vs. Stochastic Calculus
When handling stochastic processes like \( W_t \), it is tempting to differentiate them as if they were smooth functions in classical calculus. However, this naive approach fails because \( W_t \) is not differentiable in the conventional sense.
Consider the function \( t \mapsto W_t^2 \). In classical calculus, one would write:
\[ \frac{d}{dt}[W_t^2] = 2 W_t \cdot \frac{dW_t}{dt}. \]
However, since \( W_t \) is Brownian motion, the derivative \( \frac{dW_t}{dt} \) does not exist in the usual sense. A different method is needed—this is where Itô calculus comes into play.
Itô's Formula
Itô's formula is the stochastic counterpart to the classical differentiation rule. For a smooth function \( g(t, W_t) \), meaning it is twice continuously differentiable with respect to \( W_t \) and once with respect to \( t \), the formula is:
\[ dg(t, W_t) = \frac{\partial g}{\partial t} dt + \frac{\partial g}{\partial W_t} dW_t + \frac{1}{2} \frac{\partial^2 g}{\partial W_t^2} (dW_t)^2. \]
The terms have the following interpretations:
- Drift: \( \frac{\partial g}{\partial t} dt \), the classical derivative with respect to time.
- Stochastic term: \( \frac{\partial g}{\partial W_t} dW_t \), representing the variation due to Brownian motion.
- Covariation term: \( \frac{1}{2} \frac{\partial^2 g}{\partial W_t^2} (dW_t)^2 \), an additional term compared to classical calculus.
In Itô calculus, \( (dW_t)^2 = dt \), reflecting the variance of Brownian motion over an infinitesimal time interval.
Application of Itô's Formula: \( W_t^2 \)
To illustrate, consider \( g(t, W_t) = W_t^2 \). Applying Itô's formula step by step:
Step 1: Calculate Partial Derivatives
- \( \frac{\partial g}{\partial t} = 0 \) (no explicit \( t \)-dependence).
- \( \frac{\partial g}{\partial W_t} = 2 W_t \).
- \( \frac{\partial^2 g}{\partial W_t^2} = 2 \).
Step 2: Apply Itô's Formula
\[ d(W_t^2) = 0 \cdot dt + 2 W_t \cdot dW_t + \frac{1}{2} \cdot 2 \cdot (dW_t)^2. \]
Step 3: Simplify
\[ d(W_t^2) = 2 W_t \cdot dW_t + dt. \]
Integrating Itô's Formula
Integrating from 0 to \( t \), we obtain:
\[ W_t^2 = W_0^2 + 2 \int_0^t W_s \, dW_s + t. \]
If \( W_0 = 0 \), this simplifies to:
\[ W_t^2 = 2 \int_0^t W_s \, dW_s + t. \]
The intuition behind Itô's formula lies in the turbulent nature of Brownian motion. Unlike smooth paths in classical calculus, Brownian motion's paths oscillate rapidly and unpredictably. Itô's formula accounts for these irregularities by introducing the additional covariation term \( \frac{1}{2} \frac{\partial^2 g}{\partial W_t^2} (dW_t)^2 \). For \( W_t^2 \), this term manifests as the "extra" \( t \)-term, representing the cumulative variance of Brownian motion over time.

About the Author
Florian Campuzan, a graduate of Sciences Po Paris (Economic and Financial section) with a degree in Economics (money and finance), is a CFA charterholder and AMF-certified professional. He began his career in private equity and venture capital as an investment manager at Natixis before transitioning to market finance as a proprietary trader. In the early 2010s, he founded Finance Tutoring, specializing in market and corporate finance training and consulting.
For over 12 years, Florian has led finance training, advised financial institutions and industrial groups on managing risks, and prepared candidates for the CFA exam. Passionate about quantitative finance and the application of mathematics, he focuses on making complex concepts intuitive, believing that mastering any topic starts with understanding its core intuition.

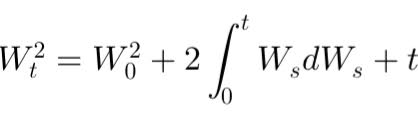
Écrire commentaire