L'inégalité de Tchebychev est un théorème fondamental en théorie des probabilités qui peut être appliqué dans divers domaines, y compris la finance quantitative.
Cette inégalité permet de comprendre la dispersion d'une distribution de probabilité. Elle stipule que pour tout nombre réel k > 0, la probabilité qu'une variable aléatoire s'écarte de plus de k écarts-types de sa moyenne est au plus de 1/k².
De plus, si X est une variable aléatoire discrète avec une fonction de masse de probabilité f(x), une moyenne μ et une variance σ², alors pour tout nombre réel, l'inégalité de Tchebychev peut être appliquée pour estimer la dispersion de cette distribution discrète. Cela augmente son utilité dans le contexte des ensembles de données discrets couramment rencontrés en finance et en économie.
Elle s'exprime comme suit : P(|X - μ| ≥ kσ) ≤ 1/k²
Ici, P est la probabilité, X est la variable aléatoire, μ (mu) est la moyenne, σ (sigma) est l'écart-type, et k est tout nombre réel positif.
L'inégalité de Tchebychev peut être utilisée pour évaluer les risques d'investissement. Elle permet d'estimer la probabilité que le rendement d'une action s'écarte de plus d'un certain pourcentage de son rendement moyen. Elle aide également à l'allocation d'actifs en comprenant les probabilités de rendements extrêmes et s'avère utile pour comprendre les limites des pertes ou gains dans des conditions de marché extrêmes.
L'avantage de l'inégalité de Tchebychev est qu'elle ne nécessite pas l'hypothèse de distribution normale, ce qui la rend polyvalente pour les instruments financiers.
Son inconvénient est qu'elle fournit une estimation conservatrice, pouvant surestimer la probabilité de résultats extrêmes, ce qui peut conduire à des stratégies excessivement prudentes.
Considérons une action avec un rendement moyen de 8 % et un écart-type de 5 %.
Objectif : Estimer la probabilité que le rendement de l'action s'écarte de plus de 10 % de sa moyenne.
Avec k = 2 (car une déviation de 10 % correspond à 2 écarts-types), l'inégalité de Tchebychev indique que P(|X - 8 %| ≥ 10 %) ≤ 1/4.
Cela implique qu'il y a au plus 25 % de chances que le rendement de l'action s'écarte de plus de 10 % de sa moyenne.
L'inégalité de Tchebychev peut être un outil utile en finance quantitative dans le cadre de l'évaluation des risques et la gestion de portefeuille. Cependant, sa nature conservatrice signifie qu'elle doit être utilisée en complément d'autres méthodes pour une analyse financière complète.
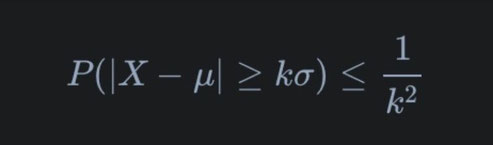
Écrire commentaire