How to derive delta for a Non-Dividend-Paying European Call Option in Simple Terms

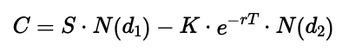
To derive \( \Delta \) for a non-dividend-paying European call option, we look at the Black-Scholes formula for a call option's price:

\[ C = S \cdot N(d_1) - K \cdot e^{-rT} \cdot N(d_2) \]

In this formula:

• \( C \): Call option price
• \( S \): Current stock price
• \( K \): Option's strike price
• \( T \): Time until the option expires
• \( r \): Risk-free interest rate
• \( N() \): Cumulative distribution function for the standard normal distribution

The values \( d_1 \) and \( d_2 \) are calculated by:

\[ d_1 = \frac{\ln(S/K) + \left(r + \sigma^2 / 2\right) \cdot T}{\sigma \cdot \sqrt{T}}, \quad d_2 = d_1 - \sigma \cdot \sqrt{T} \]

\( \Delta \), the delta for a call option, measures how much the price of the option changes if the stock price changes by one unit. To find \( \Delta \), we take the derivative of \( C \) with respect to \( S \):

\[ \Delta = \frac{dC}{dS} \]

Differentiating the Black-Scholes Formula

Differentiate the Black-Scholes formula with respect to \( S \):

\[ \Delta = \frac{d(S \cdot N(d_1))}{dS} - \frac{d(K \cdot e^{-rT} \cdot N(d_2))}{dS} \]

The derivative of \( S \cdot N(d_1) \) is:

\[ \frac{d}{dS} \left[S \cdot N(d_1)\right] = N(d_1) + S \cdot N'(d_1) \cdot \frac{d(d_1)}{dS} \]

For \( K \cdot e^{-rT} \cdot N(d_2) \), the derivative with respect to \( S \) is:

\[ \frac{d}{dS} \left[K \cdot e^{-rT} \cdot N(d_2)\right] = K \cdot e^{-rT} \cdot N'(d_2) \cdot \frac{d(d_2)}{dS} \]

Since \( d_2 = d_1 - \sigma \cdot \sqrt{T} \), we have \( \frac{d(d_1)}{dS} = \frac{d(d_2)}{dS} \), and \( N'(d_1) = N'(d_2) \). Substituting these into the equation:

\[ \Delta = N(d_1) + S \cdot N'(d_1) \cdot \frac{d(d_1)}{dS} - K \cdot e^{-rT} \cdot N'(d_2) \cdot \frac{d(d_2)}{dS} \]

Simplify further:

\[ \Delta = N(d_1) + S \cdot N'(d_1) \cdot \frac{d(d_1)}{dS} - S \cdot e^{-rT} \cdot N'(d_2) \cdot \frac{d(d_2)}{dS} \]

The \( S \cdot N'(d_1) \cdot \frac{d(d_1)}{dS} \) and \( S \cdot e^{-rT} \cdot N'(d_2) \cdot \frac{d(d_2)}{dS} \) terms cancel, leaving:

\[ \Delta = N(d_1) \]

\( N'(d_1) \) is the probability density function for the standard normal distribution, which is the derivative of \( N(d_1) \). When multiplied by \( \frac{d(d_1)}{dS} \), the \( S \) terms cancel out, simplifying to \( N(d_1) \). This reflects the risk-neutral probability of the option ending in the money, adjusted for the sensitivity of the option's price to the stock price.