In statistical analysis, particularly in regression models, two terms frequently cause confusion: heteroskedasticity and autocorrelation. Both significantly influence the interpretation and effectiveness of statistical models.
Heteroskedasticity arises when the assumption of constant variance in the residuals of a regression model is violated. This means that for different values of an independent variable, the
variance of the residuals (errors) of the dependent variable is not the same.
Imagine a model predicting property values (dependent variable) based on their size (independent variable). In a heteroskedastic scenario, the prediction errors vary more for larger properties than for smaller ones. This inconsistent error variance across different property sizes undermines the homoskedasticity assumption crucial in linear regression models.
\[ Var(\varepsilon_i) \neq \sigma^2 \]
Why worry about heteroskedasticity? It primarily affects the reliability of the model's standard errors. If not addressed, it can lead to inaccurate conclusions about the statistical significance of predictors, resulting in misleading inferences.
Autocorrelation , or serial correlation, refers to the situation where residuals in a regression model are correlated with each other over time. This is a common feature in time-series
data.
For instance, in analyzing financial market trends, today's stock price might be correlated with yesterday's price. This time-based correlation of errors breaches the independence assumption of standard regression models, leading to flawed estimations of coefficients and their standard errors.
\[ Cov(\varepsilon_t, \varepsilon_{t-1}) \neq 0 \]
The essence of heteroskedasticity lies in the varying variance of residuals across different levels of an independent variable, indicating inconsistent variability in the dependent variable.
Autocorrelation, conversely, deals with the correlation of residuals over time, indicating a dependency in the sequence of data.
Detecting and addressing these phenomena are crucial. Heteroskedasticity can be identified through tests like Breusch-Pagan, and addressed using robust standard errors or transforming
variables. Autocorrelation can be detected using the Durbin-Watson test and addressed by adjusting the model to include lagged variables or using specific time-series models.
Breusch-Pagan test: \[ H_0: \text{Homoskedasticity}, \quad H_1: \text{Heteroskedasticity} \]
Durbin-Watson test: \[ DW = 2(1 - \hat{\rho}) \]
Heteroskedasticity signals a problem with the variability of errors across different data levels, while autocorrelation points to a time sequence dependency. Recognizing and correcting these issues ensures the reliability and validity of your quantitative analyses, leading to sounder conclusions and decision-making.

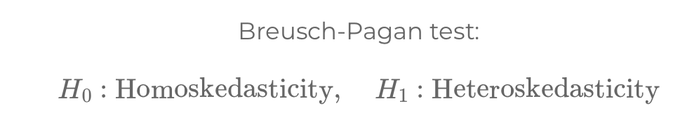
Écrire commentaire