Le taux spot \( r_n \) est le taux d'intérêt utilisé pour actualiser un flux de trésorerie sans risque reçu dans \( n \) années. Il représente le rendement d'une obligation zéro-coupon arrivant à échéance dans \( n \) années.
Imaginez que vous investissiez 100 aujourd'hui et que vous sachiez que dans 3 ans, avec un taux spot annuel de 5 %, votre investissement atteindra :
\[ 100 \times (1.05)^3 = 115.76 \]
Cela signifie que le taux spot à 3 ans \( r_3 \) est de 5 %.
Cependant, sur les marchés financiers, les taux spots ne sont pas toujours disponibles pour chaque maturité. En revanche, le marché fournit généralement des taux par—le rendement
actuariel (YTM) des obligations à coupon émises à 100.
Question : comment déduire les taux spots manquants \( r_1 \) et \( r_2 \) ?
Comme les obligations zéro-coupon sont rarement disponibles, il est nécessaire d'extraire les taux spots à partir des obligations à coupon tout en respectant un cadre sans arbitrage.
Un objectif naturel pour déterminer différents taux spots est d'identifier les opportunités d'arbitrage. Si une obligation est mal évaluée par rapport à l'actualisation théorique utilisant les
taux spots, on pourrait exploiter cette inefficacité en achetant ou en vendant l'obligation en conséquence.
En pratique, différents instruments sont utilisés pour extraire les taux spots selon les marchés :
Aux États-Unis, les titres du Trésor comme les Treasury bills (T-bills), Treasury notes et Treasury bonds sont utilisés. Les T-bills, qui sont des instruments zéro-coupon à court terme,
fournissent des points de données précis pour le début de la courbe, tandis que les Treasury notes et bonds permettent d'étendre la courbe aux échéances plus longues.
En Europe, la courbe OIS (Overnight Index Swap) est souvent utilisée comme proxy du taux sans risque pour construire la courbe d'actualisation.
Comme les obligations zéro-coupon sont rarement négociées, les meilleures données disponibles proviennent des obligations à taux par (émises à 100 et versant des coupons annuels).
Point clé : Le taux par contient toutes les informations nécessaires pour extraire les taux spots.
- Une obligation zéro-coupon ne paie qu'un montant unique à l'échéance.
- Une obligation à taux par verse des coupons périodiques plus 100 à l'échéance.
- Le marché valorise efficacement les obligations à taux par, ce qui signifie que leurs prix intègrent les informations sur les taux spots.
Cela permet d'extraire les taux spots de manière itérative grâce à une méthode appelée bootstrapping.
Le processus de bootstrapping
Nous utilisons des obligations à taux par de maturité croissante pour extraire les taux spots étape par étape.
Extraction de \( r_1 \) à partir d'une obligation à 1 an
Considérons une obligation à 1 an émise à 100 avec un coupon annuel égal à son rendement actuariel \( y_1 \) :
\[ 100 = \frac{y_1 + 100}{1 + r_1} \]
Étant donné que l'obligation est émise au pair (100), son taux par \( y_1 \) est aussi son taux spot à 1 an \( r_1 \) :
\[ r_1 = y_1 \]
Premier taux spot = taux par à 1 an.
Extraction de \( r_2 \) à partir d'une obligation à 2 ans
Prenons maintenant une obligation à 2 ans émise à 100 qui paie un coupon annuel \( y_2 \) :
\[ 100 = \frac{y_2}{1 + r_1} + \frac{y_2 + 100}{(1 + r_2)^2} \]
Étant donné que nous avons déjà calculé \( r_1 \) à l'étape précédente, nous le substituons ici.
Nous résolvons pour \( r_2 \).
Deuxième taux spot = extrait de l'obligation à 2 ans en utilisant \( r_1 \).
Extraction de \( r_3 \) à partir d'une obligation à 3 ans
Enfin, considérons une obligation à 3 ans émise à 100, versant un coupon \( y_3 \) :
\[ 100 = \frac{y_3}{1 + r_1} + \frac{y_3}{(1 + r_2)^2} + \frac{y_3 + 100}{(1 + r_3)^3} \]
Nous avons déjà résolu pour \( r_1 \) et \( r_2 \).
Nous résolvons pour \( r_3 \).
Si le \( r_3 \) calculé correspond à notre taux spot connu de 5 % à 3 ans, notre processus est validé.
Troisième taux spot = extrait de l'obligation à 3 ans en utilisant \( r_1 \) et \( r_2 \).
Connaître la courbe des taux spots est essentiel pour évaluer correctement les instruments à revenu fixe.
De plus, une fois les taux spots déterminés, les **taux forward** peuvent être dérivés en appliquant le principe de non-arbitrage. Étant donné que les taux spots intègrent la valeur temporelle de
l'argent, ils permettent de calculer des taux forward utilisés pour le pricing des produits dérivés.
1 La courbe OIS est privilégiée car elle reflète des taux quasi sans risque basés sur le financement interbancaire sécurisé, contrairement aux obligations d'État qui peuvent comporter
des risques additionnels.
🎓 Formation recommandée : Les fondamentaux du risque et dérivés de taux
Maîtrisez les concepts clés du risque de taux, découvrez les instruments dérivés associés et apprenez à les utiliser pour couvrir et gérer les risques financiers.
Découvrir la formation

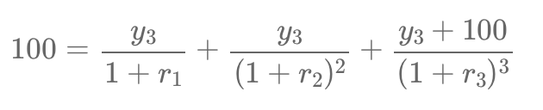
Écrire commentaire