Prime numbers are like the building blocks of all whole numbers—integers greater than 1 that have no divisors other than 1 and themselves. Examples include 2, 3, 5, and 7 (note that 2 is the only even prime number).
But how do we know there are infinitely many primes 1 ? Euclid, the great Greek mathematician, provided a beautiful argument to prove that they are endless.
Let’s suppose we have a complete, finite list of all prime numbers: \( p_1, p_2, \dots, p_k \). For example, this list could be 2, 3, 5, ... up to some last prime \( p_k \). If our assumption is correct, no more primes exist beyond this list.
We construct a new number, \( N \), by multiplying all the primes in our list together and adding 1:
\[ N = p_1 \cdot p_2 \cdot p_3 \cdot \dots \cdot p_k + 1 \]
For example, if our primes are 2, 3, and 5, then:
\[ N = 2 \cdot 3 \cdot 5 + 1 = 30 + 1 = 31 \]
This number \( N \) has two key properties:
- \( N \) is greater than any prime in our list.
- \( N \) is not divisible by any of the primes in our list.
If you divide \( N \) by any prime \( p_i \) from the list, the remainder is 1. This is because:
\[ N = (p_1 \cdot p_2 \cdot \dots \cdot p_k) + 1 \]
The product part, \( p_1 \cdot p_2 \cdot \dots \cdot p_k \), is exactly divisible by \( p_i \), but adding 1 leaves a remainder of 1.
This leads to a contradiction. If our list was supposed to contain all primes, then we shouldn’t be able to find a number like \( N \) that either is a new prime or has a new prime factor. But we did. Hence, our assumption of finitely many primes must be false.
Therefore, there must be infinitely many prime numbers.
1 Euclid’s argument for the infinitude of primes is a classic example of a proof by contradiction, relying on the properties of divisibility and remainders.

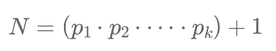
Écrire commentaire