Imagine a bag filled with different colored balls: red, blue, green, and yellow. If you know that almost all the balls are red with only a few of other colors, it's quite predictable that you'll pick a red ball if you reach in without looking. Here, we can say the entropy or randomness is low because of the high predictability.
Now, if the bag has an equal number of each color, the outcome of picking a ball becomes less predictable, indicating higher entropy or disorder.
In the world of finance, this concept of entropy is applied to portfolios containing different assets. A portfolio with low entropy is similar to the bag mostly filled with red balls - it's heavily concentrated in certain assets or sectors, making it highly sensitive to their specific movements. Higher entropy in a portfolio, akin to the bag with an equal mix of colored balls, indicates diversification.
Let’s take a portfolio with 3 different stocks (A, B, and C), each with different allocations:
Stock A: 50% (0.5)
Stock B: 30% (0.3)
Stock C: 20% (0.2)
We calculate the entropy of this portfolio using the formula:
\( H(P) = -\sum w_i \log(w_i) \)
Plugging in our weights:
\( H(P) = -[0.5 \log(0.5) + 0.3 \log(0.3) + 0.2 \log(0.2)] = 0.446 \)
So, the entropy is 0.446. Higher values of entropy (closer to 1) would mean the portfolio is more diversified, while lower values (closer to 0) indicate concentration and potentially higher risk tied to specific assets.
The entropy formula:
\( H(P) = -\sum (w_i) \log(w_i) \)
derives from the concept of entropy in information theory, originally developed by Claude Shannon. In this context, entropy measures the amount of uncertainty or disorder associated with a set of
probabilities.
\( w_i \) represents the weight of each asset in the portfolio.
\( \log(w_i) \) of the weight is used to measure the "information content" associated with each asset. An asset with lower weight (probability) contains more "information" because it's less
likely to be selected or invested in1. The logarithm function increases slowly and is always concave, emphasizing the impact of smaller probabilities.
1 In information theory, events that occur less frequently carry more “information” when they do occur. This is because they are less predictable, and observing such an event gives us more “new” information.
\( (w_i) \cdot \log(w_i) \) calculates the expected information content for each asset in the portfolio.
The sum term \( -\sum (w_i) \cdot \log(w_i) \) aggregates the expected information content across all assets in the portfolio, giving a total measure of the portfolio's "information content" or
uncertainty.
The formula naturally rewards diversification and penalizes concentration. If all assets have equal weights, there’s a higher level of uncertainty about which asset will impact the portfolio’s overall performance at any given time.

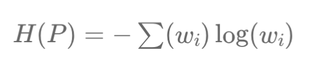
Écrire commentaire