Du noyau mathématique à son rôle en finance expliqué simplement

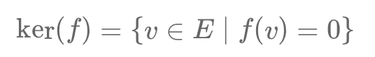
Le noyau est un concept fondamental de l’algèbre linéaire, au cœur de l’analyse des transformations linéaires. Dans un cadre mathématique général, il désigne l’ensemble des vecteurs d’un espace vectoriel qui sont envoyés sur le vecteur nul par une application linéaire. En d’autres termes, le noyau représente les éléments “annulés” par cette transformation, formant un sous-espace vectoriel. Cet article explore la définition mathématique du noyau, son interprétation géométrique et son rôle pratique dans les modèles financiers.

Le Noyau : Cadre Mathématique et Propriétés

Formellement, le noyau d’une application linéaire \( f \), noté \( \text{ker}(f) \), est défini comme l’ensemble des vecteurs \( v \) appartenant à \( E \) tels que :

Ce sous-espace vectoriel contient tous les vecteurs “écrasés” par la transformation \( f \). Par exemple, si une projection envoie un espace tridimensionnel sur un plan, le noyau contient les vecteurs orthogonaux à ce plan. La dimension du noyau joue un rôle clé : elle détermine combien de directions de l’espace original sont réduites à zéro.

Cette relation est encadrée par le théorème du rang, qui stipule :

Dans le cas d’une matrice \( A \) représentant une application linéaire, le noyau correspond à l’ensemble des solutions de :

Géométriquement, ce noyau représente les vecteurs qui restent dans un sous-espace invariant sous l’action de \( A \). Si :

alors \( A \) est injective¹, c’est-à-dire qu’elle ne perd aucune information.

Noyau et Modèles Financiers

Dans les modèles financiers, le noyau révèle des inefficacités, des redondances ou des pertes d’information. Un exemple courant se trouve dans l’analyse des actifs corrélés. Considérons une matrice de covariance \( \Sigma \), souvent utilisée en gestion de portefeuille pour modéliser les relations entre actifs financiers. Si \( \Sigma \) est une matrice carrée représentant les variances et covariances des rendements, elle agit comme une application linéaire qui transforme les pondérations \( w \) en un vecteur représentant le risque.

Cette transformation s’écrit :

Le noyau de \( \Sigma \), noté \( \text{ker}(\Sigma) \), contient les vecteurs \( w \) tels que :

Ces vecteurs représentent des combinaisons linéaires d’actifs parfaitement corrélés ou redondants, formant des portefeuilles qui n’ajoutent aucun risque. Si :

cela indique des relations linéaires entre certains actifs, traduisant une redondance dans les données.

Rendements et Portefeuilles Constants

Un autre exemple se trouve dans la transformation des valeurs d’actifs en rendements relatifs. Si \( P \) représente un vecteur de valeurs, une transformation linéaire typique est :

où \( P_0 \) est le vecteur des valeurs initiales. Le noyau de cette transformation est constitué des portefeuilles tels que :

Ils correspondent à des portefeuilles constants sans variation de valeur et donc sans rendements mesurables.

Optimisation de Portefeuille

Le noyau joue également un rôle dans des contextes complexes comme l’optimisation de portefeuille basée sur la théorie de Markowitz. Si \( \Sigma \) est mal conditionnée (par exemple, si certains actifs sont fortement corrélés), son noyau identifie les directions dans l’espace des pondérations qui n’affectent pas le risque total. Cela simplifie les calculs et met en évidence les facteurs redondants.

Le noyau a des implications concrètes et puissantes en finance. Il permet d’identifier des pertes ou redondances d’information dans les modèles financiers et fournit un cadre rigoureux pour l’optimisation de portefeuille et l’analyse des relations entre actifs.

¹ Une application linéaire est dite injective si :

Autrement dit, des vecteurs distincts dans l’espace de départ restent distincts dans l’espace d’arrivée.