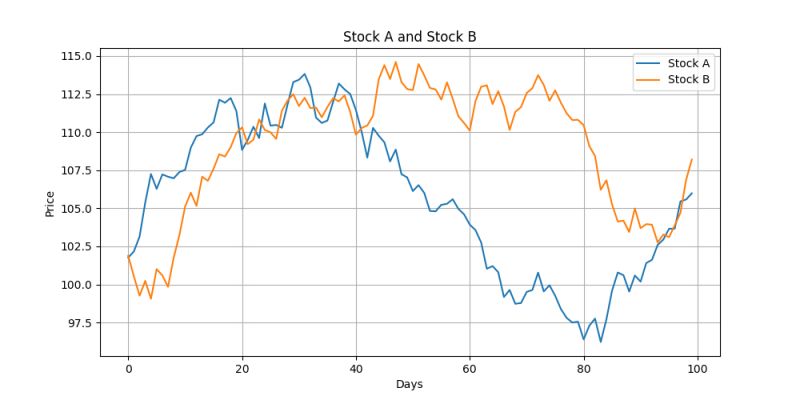
Supposons que nous analysions deux actions, l'Action A et l'Action B, pour rechercher des opportunités de trading de paires. La première étape consiste à examiner la distribution marginale de chaque action.
Après une analyse détaillée, nous découvrons que l'Action A suit une distribution normale avec un rendement moyen de 5 % et un écart-type de 2 %. Cette distribution marginale donne des indications sur les rendements attendus et la volatilité de l'Action A individuellement.
L'Action B, quant à elle, présente une distribution marginale qui est asymétrique à droite, indiquant qu'elle a parfois généré des rendements élevés, bien que son rendement moyen soit également d'environ 5 %.
Nous nous intéressons maintenant à comprendre le comportement de l'Action A compte tenu de la performance de l'Action B et inversement.
Supposons que, les jours où les rendements de l'Action B dépassent son rendement moyen de 5 %, l'Action A a tendance à sous-performer, affichant des rendements inférieurs à sa moyenne. Nous calculons alors la distribution conditionnelle des rendements de l'Action A, compte tenu de la performance de l'Action B dépassant ses rendements moyens.
Lorsque les rendements de l'Action B devraient être supérieurs à 5 %, le trader pourrait envisager de vendre à découvert l'Action A, s'attendant à ce qu'elle sous-performe en raison de la relation conditionnelle observée.
Les distributions marginales donnent au trader des informations sur le comportement individuel de chaque action, tandis que la distribution conditionnelle éclaire les interdépendances entre les deux actions.
Par exemple, si la performance de l'Action B dépasse les attentes, la distribution conditionnelle informe le trader sur la probabilité de sous-performance de l'Action A. Par conséquent, une stratégie de trading de paires pourrait consister à vendre l'Action A à découvert et à acheter l'Action B lorsque ce scénario se présente.
Une intégration judicieuse des deux distributions permet aux traders d’élaborer des stratégies de trading de paires nuancées et basées sur les données, optimisant la rentabilité tout en atténuant les risques.
Les copules relient les distributions marginales à la distribution conjointe et ouvrent la voie à des analyses plus avancées.
Dans le domaine des copules, les fonctions de probabilité conditionnelle jouent un rôle clé. Définies par la différenciation de la copule par rapport à ses paramètres, ces fonctions révèlent des informations détaillées sur les dépendances entre actifs.
Par exemple, considérons les probabilités conditionnelles P(U > u|V = v) et P(V > v|U = u).
Celles-ci sont calculées à l'aide des formules suivantes :
- P(U > u|V = v) = ∂C(u, v)/∂v
- P(V > v|U = u) = ∂C(u, v)/∂u
C(u, v) est la fonction de copule qui capture la dépendance entre les deux actions, et les dérivées partielles par rapport à u et v donnent les probabilités conditionnelles.
Où :
- U et V sont les distributions marginales uniformes transformées des rendements des Actions A et B, respectivement.
- "u" et "v" sont des valeurs spécifiques au sein de ces distributions.
- Par exemple, u = 0,7 représenterait le rendement de l'Action A au 70e centile de sa distribution uniforme, et v = 0,8 représenterait le rendement de l'Action B au 80e centile de sa distribution uniforme.


Écrire commentaire