The Chaos Theory simply explained

Chaos theory is a field of study in mathematics that deals with systems that appear to be disordered, but are actually following deterministic rules that are highly sensitive to initial conditions. This sensitivity causes the system to appear random and unpredictable.

One of the simplest mathematical models to demonstrate chaos is the logistic map. This is a recurrence relation which is used to model population growth and is given by:

x(n+1) = r * x(n) * (1 - x(n))

Here, x(n) is the proportion of the maximum possible population at time n, and r is a growth rate parameter.

The behavior of the system changes dramatically with different values of r.

In the chaotic regime (when r is between about 3.57 and 4) the logistic map shows how a simple deterministic system can produce random and complex structures which are actually fractals if we plot the outcomes over a range of r values. This is related to the concept of strange attractors (*) in chaos theory.

For continuous systems, like weather systems, the Lorenz equations are a set of differential equations that also exhibit chaotic behavior.

Applying this to quantitative finance, the logistic map can be used to model the non-linear dynamics of stock prices, market indices, or entire economic cycles. For example, it can represent the cyclical nature of markets, the build-up and bursting of financial bubbles, or the unpredictable movement of stock prices. These dynamics reflect the market’s sensitivity to initial conditions, akin to the sensitivity of the logistic map to its initial value of x(n).

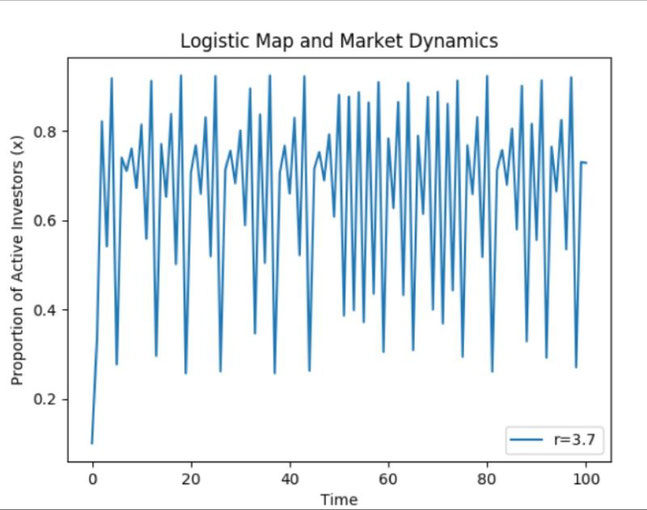
Chaos theory can be applied to model stock market dynamics by using the logistic map to simulate the behavior of active investors in the market. In this model, the proportion of active investors x(n) at discrete time intervals influences price movements. The growth rate parameter (r) represents market volatility and sentiment. As x(n) fluctuates, it indicates buying or selling pressure, which could drive prices up or down. When r exceeds 3.56995, the market behavior can become chaotic, making traditional predictions unreliable. 

This highlights the market's potential for unpredictable behavior and the importance of considering chaotic dynamics in quantitative finance. Such models can be part of a broader set of tools for developing more robust trading and risk management strategies.


(*) In the chaotic regime, the points plotted by the logistic map can form fractal patterns, revealing a strange attractor.