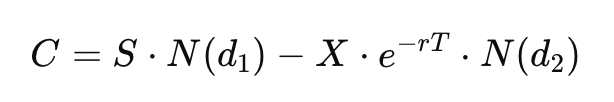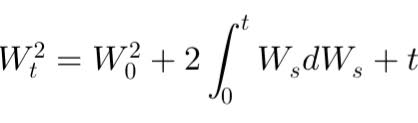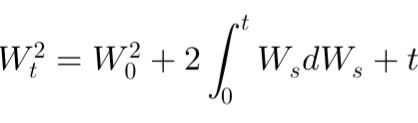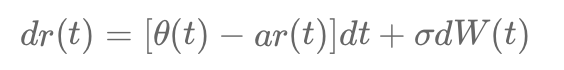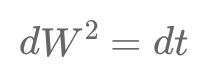Processus et Modèles Stochastiques
Processus et Modèles Stochastiques · 05. mars 2025
Dans le modèle de Black-Scholes, N(d1) et N(d2) agissent comme des indicateurs mesurant la probabilité de différents événements financiers. Imaginez un jeu où vous devez deviner si une action atteindra un certain prix. N(d1) représente votre meilleure estimation, en tenant compte des règles et des probabilités du jeu. De son côté, N(d2) indique combien vous devriez idéalement payer pour participer, en fonction de ces probabilités.
Processus et Modèles Stochastiques · 05. mars 2025
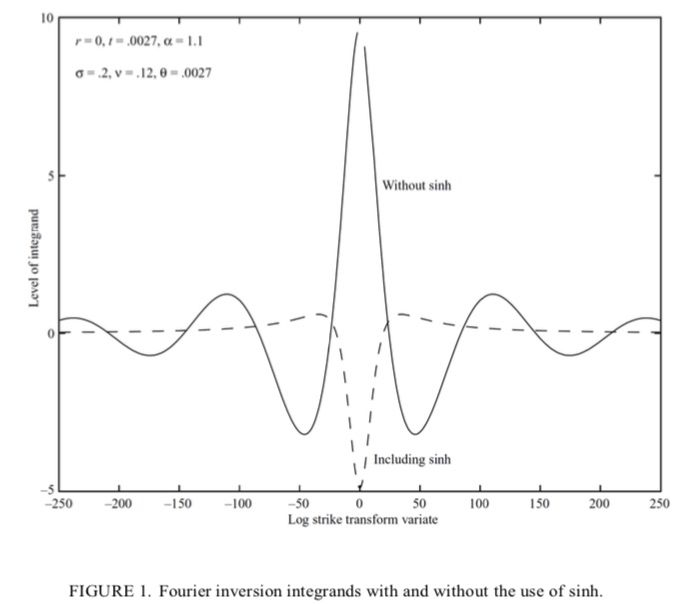
Découvrez comment la méthode de Carr & Madan exploite la transformée de Fourier pour la valorisation des options. Explorez les concepts clés, apprenez à atténuer les instabilités et améliorez les calculs numériques.
Processus et Modèles Stochastiques · 04. octobre 2024
Stochastic calculus models continuous random phenomena like asset prices, using Itô calculus to handle the unique behavior of Brownian motion. Unlike classical calculus, Itô’s formula accounts for stochastic properties, adjusting calculations to capture the volatility and irregularity of financial markets.
Processus et Modèles Stochastiques · 04. octobre 2024
Le calcul stochastique modélise les phénomènes aléatoires en continu, tels que les prix financiers. La formule d'Itô permet de différencier ces processus en tenant compte de la variance unique du mouvement brownien, apportant une perspective clé pour analyser les dynamiques de marché.
Processus et Modèles Stochastiques · 12. novembre 2023
Le modèle de Hull-White valorise les dérivés de crédit comme les CDS en utilisant un taux de défaut stochastique. Il calcule les probabilités de survie et de défaut, ajuste les primes en fonction du risque, et utilise des données de marché pour estimer la valeur actuelle des paiements conditionnels liés aux défauts.
Processus et Modèles Stochastiques · 01. novembre 2023
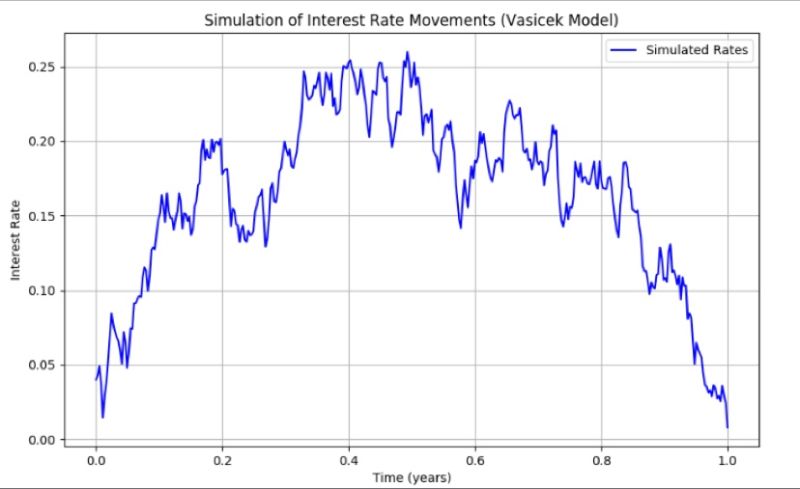
Découvrez dans cet article le modèle de Vasicek, un modèle mathématique permettant de modéliser les taux d'intérêt, à partir d'une équation différentielle stochastique. Il intègre les paramètres de retour à la moyenne, de volatilité et de vitesse de retour à cette moyenne. Il est largement utilisé pour simuler les mouvements des taux dans les marchés à revenu fixe. La formule principale est : dr(t) = κ(θ - r(t)) dt + σ dW(t).
Processus et Modèles Stochastiques · 09. octobre 2023
Quantitative finance relies on rules from stochastic calculus, like dW^2=dt, highlighting Brownian motion's unpredictability, and Zero Rules, underscoring infinitesimal term behaviors, crucial in financial modeling and risk management.
#Finance #RiskManagement
Processus et Modèles Stochastiques · 09. octobre 2023
Les règles de multiplication en calcul stochastique sont fondamentales pour modéliser les processus aléatoires, tels que le mouvement brownien, en finance quantitative. Elles permettent de comprendre les comportements de variance et d'incertitude, essentiels dans l'évaluation des options et la gestion des risques.
Processus et Modèles Stochastiques · 17. septembre 2023
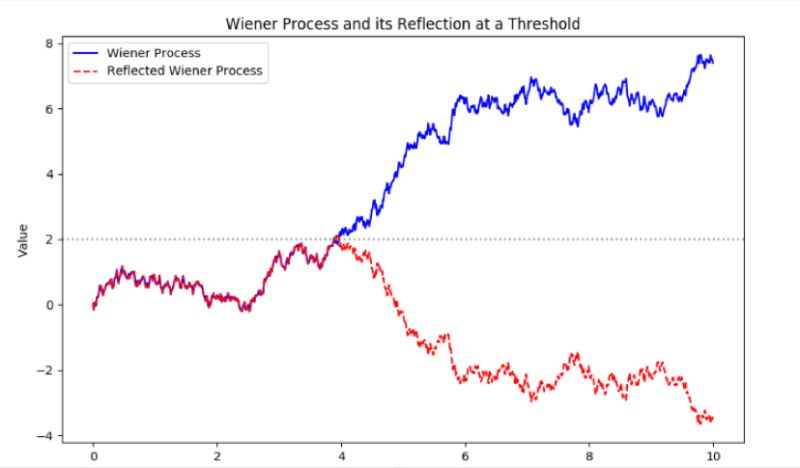
The reflection principle, illustrated by a stone's path and reflection in a lake, mirrors the Wiener process in stochastic calculations, highlighting symmetry in Brownian motion. It simplifies math in stochastic process problems, aiding in pricing barrier and lookback options. #SEO
Processus et Modèles Stochastiques · 29. juillet 2023
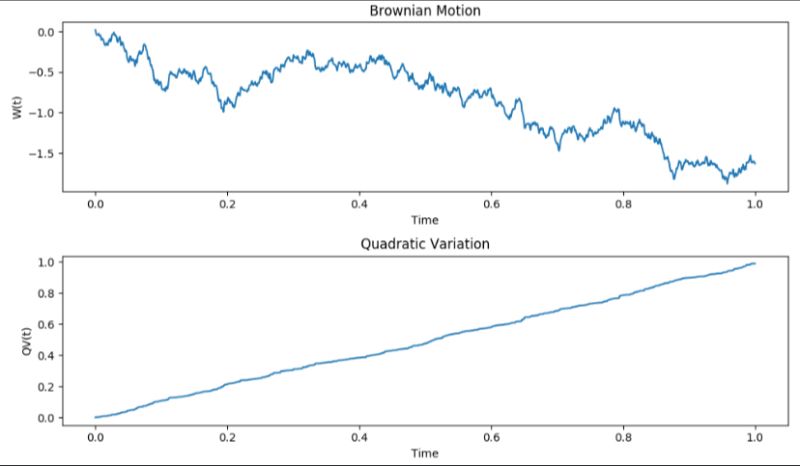
La variation quadratique en finance mesure la volatilité des mouvements de prix d’actifs, essentielle pour comprendre l'irrégularité des marchés et évaluer les risques dans le trading et la modélisation des options.