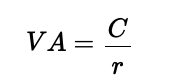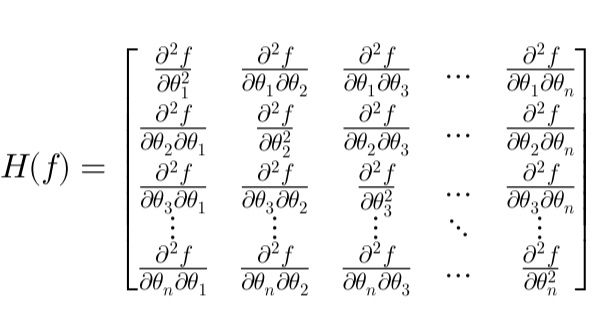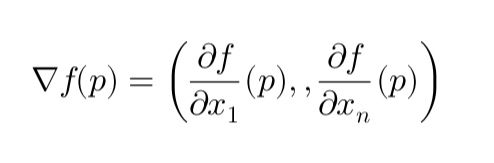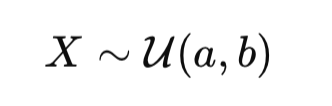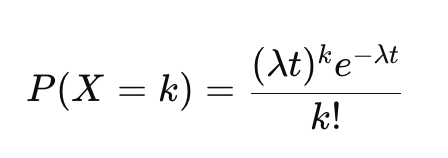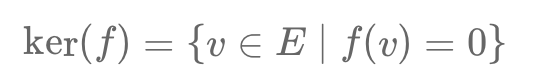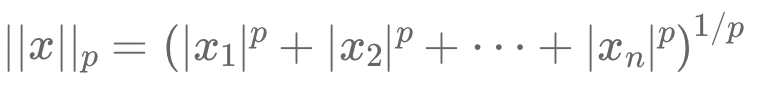Principes mathématiques et applications en finance
Principes mathématiques et applications en finance · 13. mars 2025
Une perpétuité est un instrument financier qui fournit des flux de trésorerie sans fin. Elle est utilisée pour évaluer des actions avec des dividendes fixes, l’immobilier avec des revenus stables, les obligations perpétuelles et la valorisation des entreprises. Lorsque les paiements augmentent au fil du temps, la valeur s’accroît, ce qui en fait un outil utile pour estimer des flux de trésorerie futurs en hausse.
Principes mathématiques et applications en finance · 05. mars 2025
La matrice hessienne, composée de dérivées partielles du second ordre, est un outil fondamental en optimisation financière et en valorisation des dérivés. Cet article simplifie son rôle dans l’identification des points critiques, les approximations quadratiques et la gestion des risques via le Gamma hedging.
Principes mathématiques et applications en finance · 01. mars 2025
Cet article explique la descente de gradient en termes simples, en couvrant ses bases mathématiques et ses applications en finance, notamment dans la calibration du modèle de Hull-White pour la modélisation des taux d’intérêt. Il détaille le gradient, son rôle dans l’optimisation et la manière dont il minimise les erreurs de façon itérative. Les étapes clés de la calibration de la volatilité (σ) par descente de gradient sont présentées avec un exemple pratique.
Principes mathématiques et applications en finance · 25. février 2025
La loi uniforme est un concept fondamental en finance quantitative, largement utilisée dans les simulations de Monte-Carlo, les équations différentielles stochastiques (EDS) et les modèles de copules pour l’évaluation des risques. Cet article explique comment la fonction de répartition (CDF) et son inverse transforment les probabilités en chocs standardisés, essentiels pour modéliser les mouvements des prix des actifs.
Principes mathématiques et applications en finance · 18. février 2025
La distribution de Poisson, nommée d'après Siméon-Denis Poisson, est largement utilisée dans la modélisation du risque financier pour estimer les probabilités de défaut dans les portefeuilles de prêts. Elle permet de quantifier les événements rares et d'évaluer l'exposition au risque de crédit sur une période donnée.
Pourquoi est-ce important ?
Prédit les défauts attendus pour une meilleure évaluation des risques.
Soutient les tests de résistance et l'analyse de scénarios extrêmes.
Principes mathématiques et applications en finance · 20. décembre 2024
Le noyau est un concept clé en algèbre linéaire, représentant l’ensemble des vecteurs annulés par une transformation linéaire. Il joue un rôle essentiel en finance pour analyser les matrices de covariance, optimiser les portefeuilles et réduire la dimensionnalité des données. Utilisé dans la gestion des risques et l’optimisation financière, il identifie les redondances et simplifie les modèles tout en maintenant leur précision.
Principes mathématiques et applications en finance · 20. décembre 2024
En finance et en mathématiques, de nombreuses situations nécessitent de passer d’un modèle discret, comme une somme, à une approximation continue, comme une intégrale. Ce passage permet de simplifier les calculs, de modéliser des comportements asymptotiques et de généraliser les résultats. Cependant, cette transition soulève des défis, notamment pour ajuster les différences entre les deux approches. Ces ajustements incluent souvent des corrections spécifiques, comme celles...
Principes mathématiques et applications en finance · 19. décembre 2024
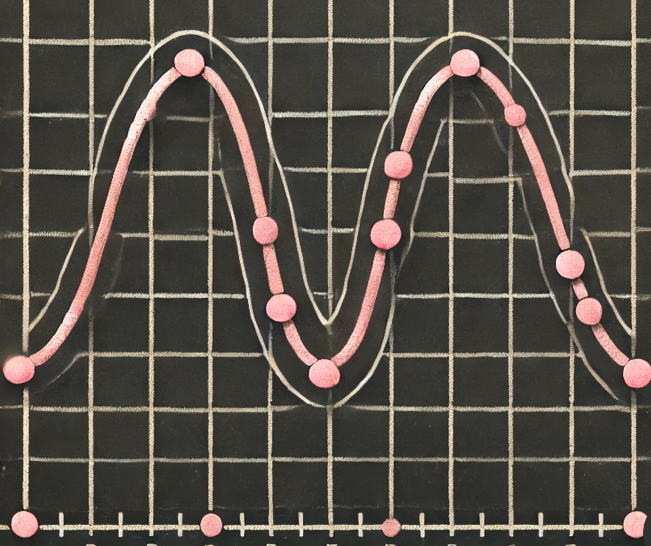
Le phénomène de Runge, identifié en 1901, survient lors de l’interpolation polynomiale avec des polynômes de degré élevé, provoquant des oscillations importantes, surtout aux extrémités de l’intervalle. En finance quantitative, cela impacte la construction de courbes de taux, les surfaces de volatilité implicite et la calibration de modèles, générant des artefacts non réalistes.
Principes mathématiques et applications en finance · 19. décembre 2024
Cet article explique le concept des normes mathématiques et leur rôle crucial en finance quantitative. Les normes mesurent la taille ou la longueur des vecteurs dans un espace vectoriel, ce qui en fait des outils essentiels pour analyser les données financières.