Market Finance
Market Finance · 19. janvier 2025
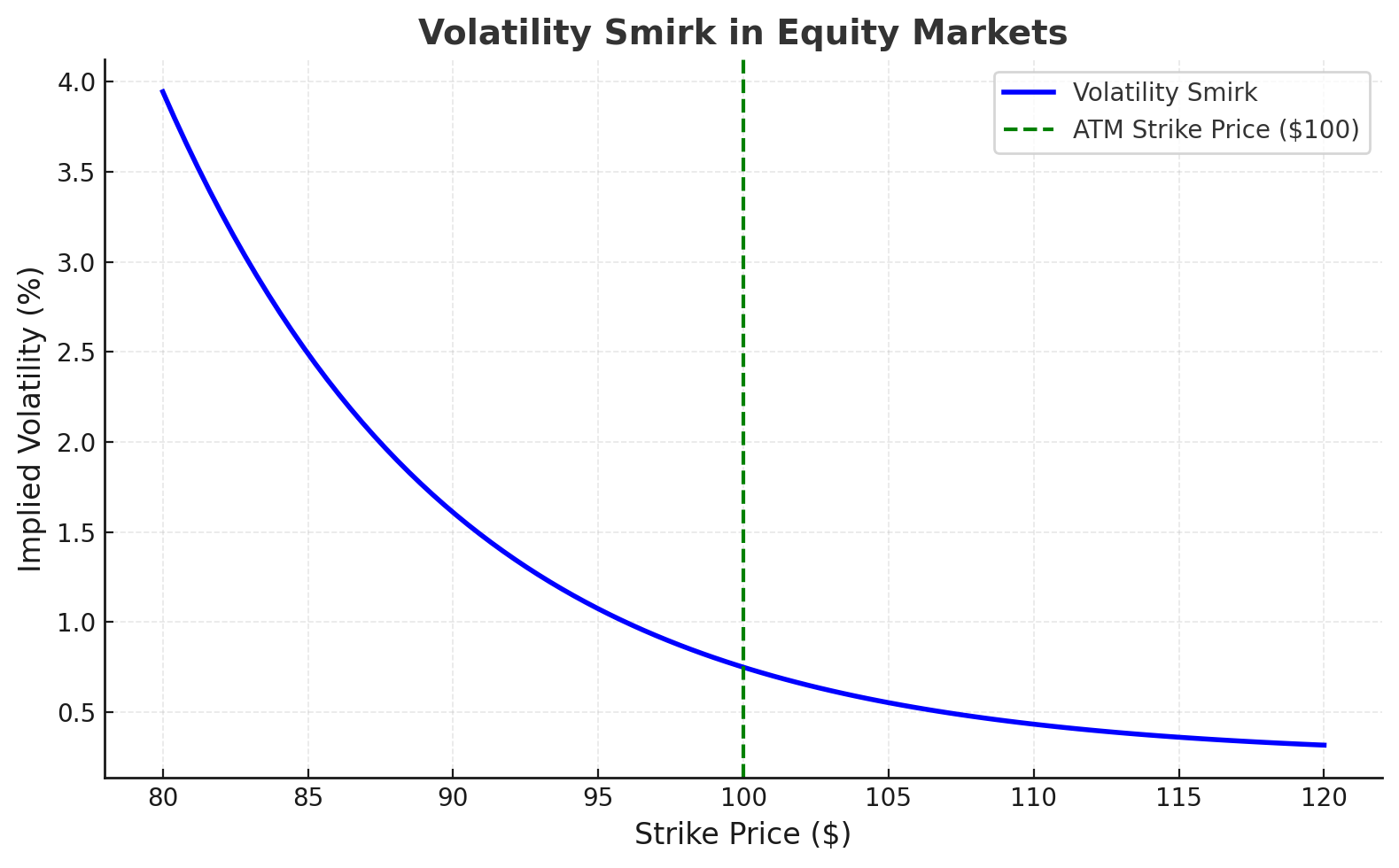
Volatility smirk is a key concept in equity options trading, reflecting higher implied volatility for out-of-the-money (OTM) puts compared to calls. Unlike the balanced "volatility smile" seen in currency markets, the smirk highlights the asymmetric risks in equities, driven by market fear, demand for downside protection, and sharp price drops during downturns. Understanding volatility smirk helps traders accurately price options, manage risks, and exploit arbitrage opportunities.
Market Finance · 19. janvier 2025
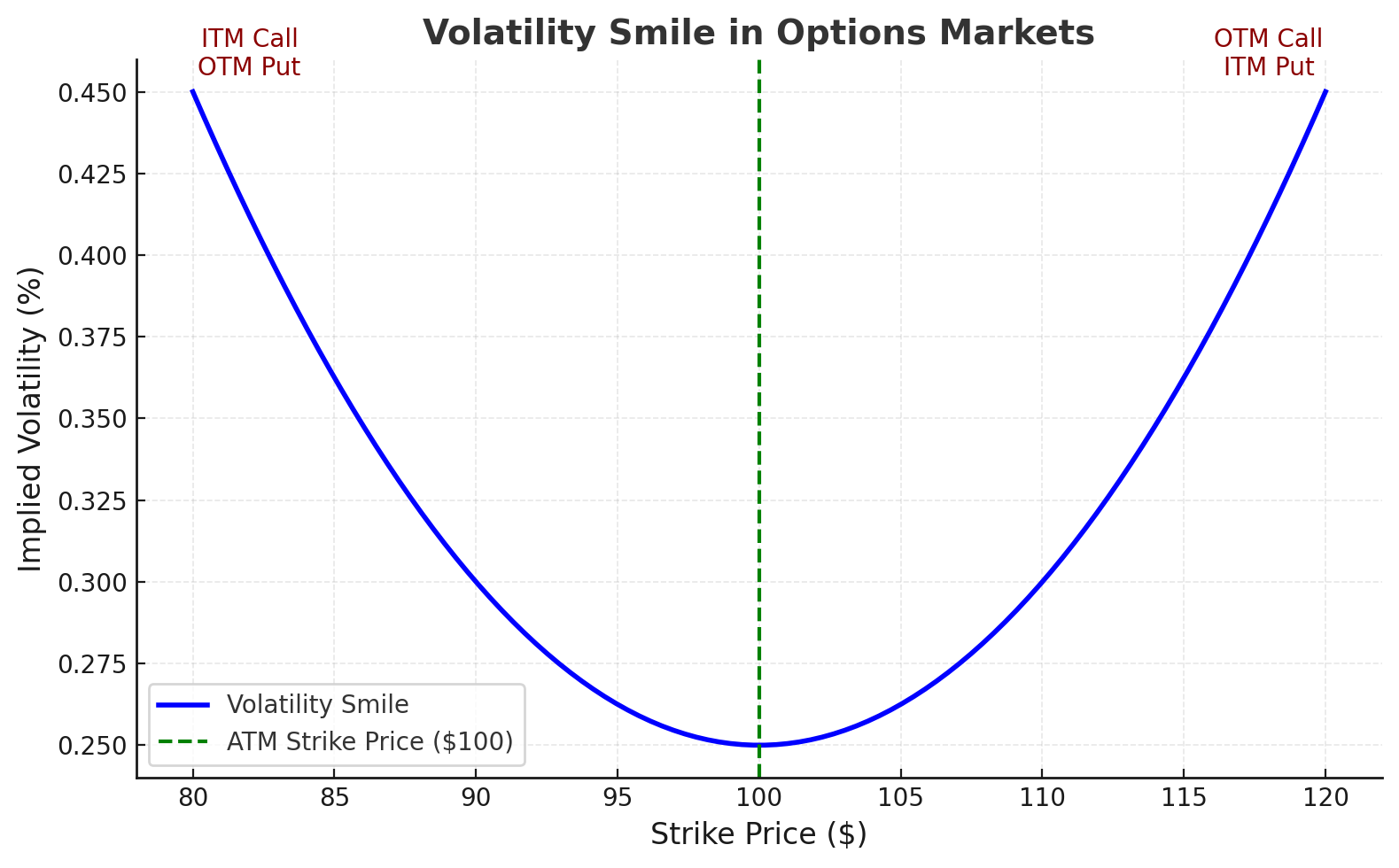
Volatility skew is a critical concept in options trading, reflecting the differences in implied volatility across various strike prices. Unlike the constant volatility assumption in the Black-Scholes model, real-world markets show skew patterns due to market fear, hedging demand, and asymmetric risks. Currency markets often exhibit a "volatility smile" due to balanced risks between appreciation and depreciation, while equity markets display a "volatility smirk".
Market Finance · 21. septembre 2024
In portfolio management, understanding "value added" (active return) is key to measuring performance relative to a benchmark. This outperformance is driven by two factors: asset allocation (how assets are distributed across classes) and security selection (the choice of specific assets). By comparing the portfolio’s return to the benchmark’s return, we calculate the total value added. Asset allocation considers how weight differences impact returns, while security selection isolates the effect
Market Finance · 13. novembre 2023
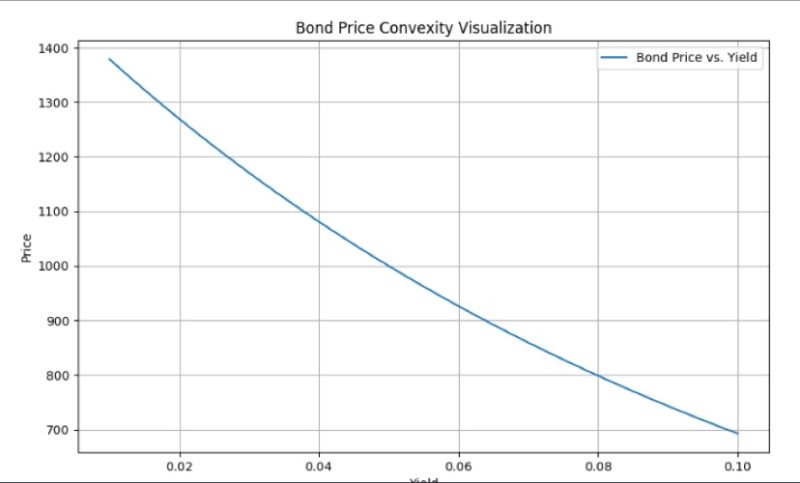
La convexité mesure la sensibilité du prix d'une obligation aux variations des taux d'intérêt, offrant une analyse plus précise que la duration. Elle permet d'anticiper des changements asymétriques de prix pour des hausses ou baisses de taux. La convexité est essentielle pour gérer le risque de taux, optimiser le prix des obligations, et est utilisée dans les stratégies de couverture en portefeuille.