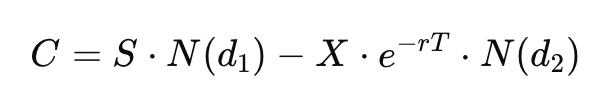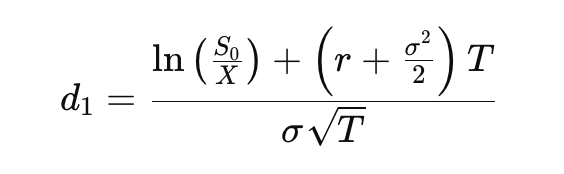Stochastic Models and Processes · 08. septembre 2023
Unpack the myth that option Delta equals the probability of expiring in-the-money. Dive into risk-neutral valuation and the Black-Scholes model, where assets grow at a risk-free rate, making Delta an unreliable real-world probability indicator. Explore the distinction for smarter option trading. #OptionTrading #BlackScholes #RiskNeutralValuation
Stochastic Models and Processes · 20. mai 2023
In the Black-Scholes model, N(d1) and N(d2) are like gauges measuring the likelihood of different financial events. Imagine a game where you're guessing if a stock will reach a certain price. N(d1) is your best guess, factoring in the game's rules and odds. Meanwhile, N(d2) is about how much you'd ideally pay to play based on those odds. Together, they help determine an option's value. Simply, N(d1) gives the winning chance, and N(d2) gauges the cost. #OptionsExplained #BlackScholesModel
Stochastic Models and Processes · 18. février 2023
The d₁ term in the Black-Scholes model captures key factors of option pricing like stock price, strike price, volatility, and time. N(d₁) represents the option's delta, showing how sensitive its price is to the stock price. While often mistaken for the probability of the option ending in the money, this is actually the role of N(d₂). N(d₁) primarily reflects the option's sensitivity and hedge ratio.