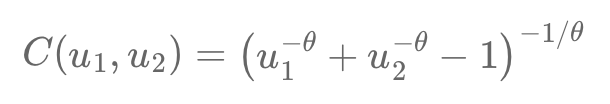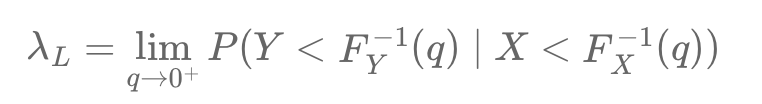Mathematical Principles and Quantitative Finance · 30. septembre 2024
Copulas help model dependencies between variables separately from their behaviors, crucial for finance's complex relationships. For example, Alice and Bob’s race times show dependency when transformed into uniform variables using cumulative distribution functions (CDFs). The Clayton copula captures asymmetric dependence, especially in lower tail risks, using the formula:
C(u1, u2) = (u1^(-θ) + u2^(-θ) - 1)^(-1/θ).
Mathematical Principles and Quantitative Finance · 28. février 2024
Risk assessment in CDOs involves probability theory for individual defaults and correlation analysis for linked defaults. CDOs have senior, mezzanine, and equity tranches with varying risks. High correlation suggests simultaneous defaults and larger losses, while low correlation indicates independent defaults, impacting different tranches.
#CDOsExplained #RiskAssessment #DefaultFrequency #ProbabilityTheory