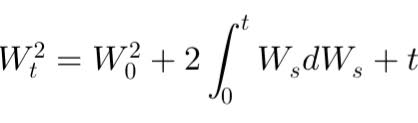Processus et Modèles Stochastiques · 04. October 2024
Stochastic calculus models continuous random phenomena like asset prices, using Itô calculus to handle the unique behavior of Brownian motion. Unlike classical calculus, Itô’s formula accounts for stochastic properties, adjusting calculations to capture the volatility and irregularity of financial markets.
Stochastic Models and Processes · 19. November 2023
Multiplying a Wiener process W_t by its integral creates a complex stochastic process, combining an instantaneous, "memoryless" state with its cumulative history. This nonlinear product, needing tools like Itô's lemma for analysis, reveals interactions between the current state and past values, crucial in financial mathematics for pricing path-dependent options.
#StochasticProcesses #ItôsLemma #StochasticCalculus #QuadraticCovariation #BrownianMotion
Stochastic Models and Processes · 12. November 2023
The Hull-White model is a credit derivative pricing tool that uses a stochastic hazard rate to reflect default risk and economic conditions. It calculates survival probabilities and expected losses to price Credit Default Swaps (CDS), employing a risk-neutral approach and calibration with market data for realistic valuation.
Stochastic Models and Processes · 03. November 2023
The Cheyette Model is a complex financial tool for predicting interest rate movements, accounting for time-varying mean reversion and volatility. It's more intricate than simpler models like Vasicek due to its detailed parameters, which makes it robust but computationally intensive and less commonly used in practice.
Stochastic Models and Processes · 01. November 2023
The Bjerksund-Stensland model modifies Black-Scholes-Merton to value American options with dividends. It calculates when to exercise early, using an "early exercise boundary." If the stock's below this, exercising might be wise; if above, holding on could be better. It factors in discrete dividends, unlike the continuous assumption in Black-Scholes.
Stochastic Models and Processes · 22. October 2023
The Cox-Ingersoll-Ross (CIR) model is essential for modeling interest rate evolution with mean reversion, variable volatility, and a square root process that precludes negative rates. Used for valuing financial instruments sensitive to rate changes, its parameters guide simulations of rate behavior. #CIRModel #InterestRates #Finance
Stochastic Models and Processes · 21. October 2023
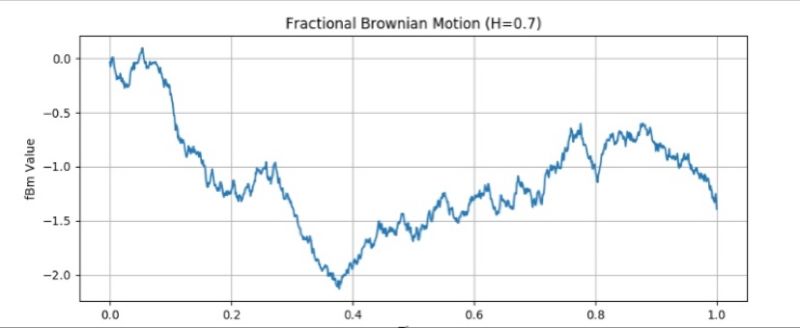
Fractional Brownian Motion (fBm) enriches classical Brownian motion by introducing the Hurst parameter (H), making it vital for modeling varying volatility in finance, physics, and beyond. With H dictating path roughness, fBm handles predictions in systems with long-range dependencies, aiding in asset volatility modeling and risk management. It's pivotal for understanding market behaviors and complex dynamics in diverse scientific fields.
Stochastic Models and Processes · 06. October 2023
GBM is essential in financial forecasting, known for capturing stock price movements and aiding in option pricing. It corrects inflated growth trajectories inherent in continuous compounding, offering a balanced price evolution. Unlike BS model, GBM adjusts expected return downwards to account for volatility, enhancing precision in financial forecasts. #Finance #Stocks #Volatility
Principes mathématiques et applications en finance · 17. September 2023
Le principe de réflexion, illustré par le cheminement d'une pierre et son reflet dans un lac, reflète le processus de Wiener dans les calculs stochastiques, mettant en lumière la symétrie du mouvement brownien. Il simplifie les calculs dans les problèmes de processus stochastiques, aidant à la tarification des options barrières et lookback.
Processus et Modèles Stochastiques · 17. September 2023
The reflection principle, illustrated by a stone's path and reflection in a lake, mirrors the Wiener process in stochastic calculations, highlighting symmetry in Brownian motion. It simplifies math in stochastic process problems, aiding in pricing barrier and lookback options. #SEO