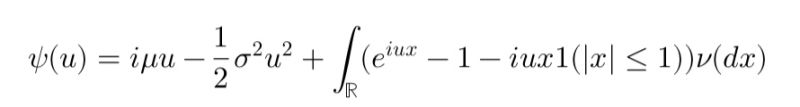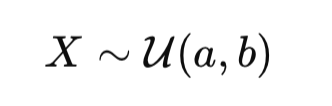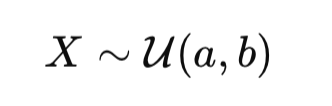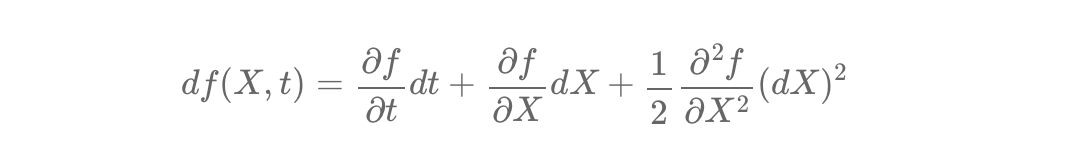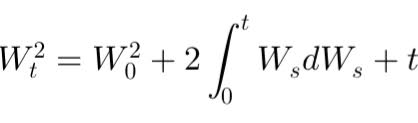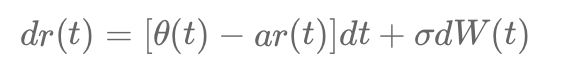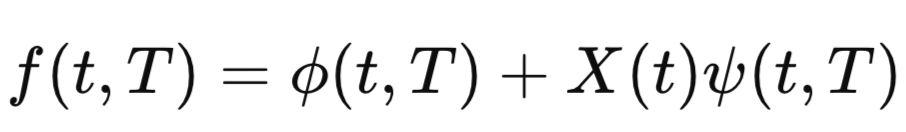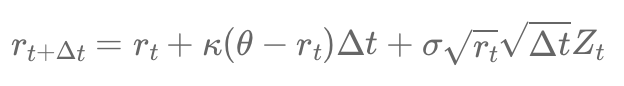Stochastic Models and Processes · 05. mars 2025
A Lévy process is a fundamental concept in probability theory and financial mathematics, extending Brownian motion by incorporating both continuous movements and discontinuous jumps. Characterized by independent and stationary increments, Lévy processes play a crucial role in modeling financial assets with sudden price changes, making them widely used in quantitative finance, risk management, and option pricing.
Principes mathématiques et applications en finance · 25. février 2025
La loi uniforme est un concept fondamental en finance quantitative, largement utilisée dans les simulations de Monte-Carlo, les équations différentielles stochastiques (EDS) et les modèles de copules pour l’évaluation des risques. Cet article explique comment la fonction de répartition (CDF) et son inverse transforment les probabilités en chocs standardisés, essentiels pour modéliser les mouvements des prix des actifs.
Mathematical Principles and Quantitative Finance · 25. février 2025
The uniform law is a fundamental concept in quantitative finance, widely used in Monte Carlo simulations, stochastic differential equations (SDEs), and copula models for risk assessment. This article explains how the cumulative distribution function (CDF) and its inverse transform probabilities into standardized shocks, essential for modeling asset price movements.
Stochastic Models and Processes · 07. janvier 2025
Taylor Expansion and Itô's Lemma are fundamental tools for modeling deterministic and stochastic systems. Taylor Expansion provides approximations for smooth and predictable systems, while Itô's Lemma adapts these principles to account for randomness, a critical feature in financial modeling.
Processus et Modèles Stochastiques · 04. octobre 2024
Stochastic calculus models continuous random phenomena like asset prices, using Itô calculus to handle the unique behavior of Brownian motion. Unlike classical calculus, Itô’s formula accounts for stochastic properties, adjusting calculations to capture the volatility and irregularity of financial markets.
Stochastic Models and Processes · 12. novembre 2023
The Hull-White model is a versatile framework for modeling short-term interest rates and credit risk. It captures the stochastic behavior of rates or hazard rates, ensuring flexibility and accuracy in pricing derivatives like bonds and Credit Default Swaps (CDS). By modeling hazard rates, the model calculates survival and default probabilities, enabling dynamic risk assessment.
Stochastic Models and Processes · 03. novembre 2023
The Cheyette Model is a complex financial tool for predicting interest rate movements, accounting for time-varying mean reversion and volatility. It's more intricate than simpler models like Vasicek due to its detailed parameters, which makes it robust but computationally intensive and less commonly used in practice.
Stochastic Models and Processes · 01. novembre 2023
The Bjerksund-Stensland model modifies Black-Scholes-Merton to value American options with dividends. It calculates when to exercise early, using an "early exercise boundary." If the stock's below this, exercising might be wise; if above, holding on could be better. It factors in discrete dividends, unlike the continuous assumption in Black-Scholes.
Stochastic Models and Processes · 01. novembre 2023
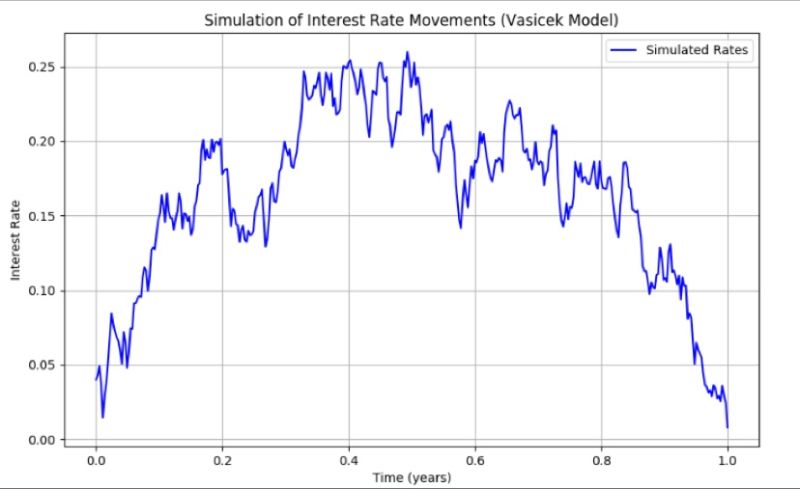
The Vasicek model predicts interest rates using mean reversion, volatility, and the speed of reversion. Its equation, dr(t) = κ(θ - r(t)) dt + σ dW(t)`, models rates' return to a mean (θ) with volatility (σ) and randomness (dW(t)). It's vital for financial strategies and simulations.
Stochastic Models and Processes · 22. octobre 2023
The Cox-Ingersoll-Ross (CIR) model is essential for modeling interest rate evolution with mean reversion, variable volatility, and a square root process that precludes negative rates. Used for valuing financial instruments sensitive to rate changes, its parameters guide simulations of rate behavior. #CIRModel #InterestRates #Finance