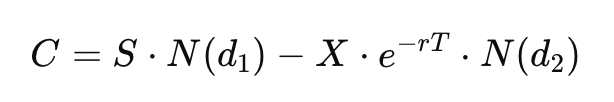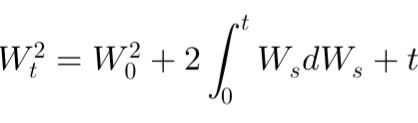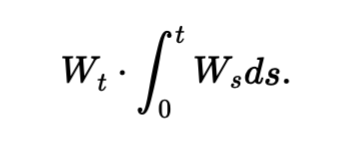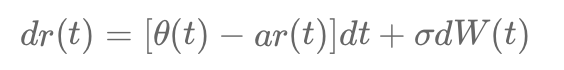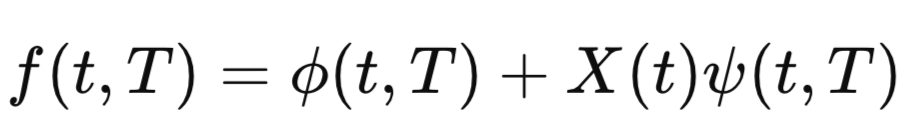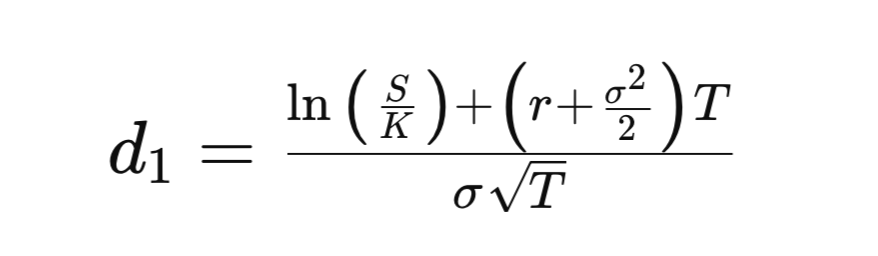Processus et Modèles Stochastiques · 04. octobre 2024
Le calcul stochastique modélise les phénomènes aléatoires en continu, tels que les prix financiers. La formule d'Itô permet de différencier ces processus en tenant compte de la variance unique du mouvement brownien, apportant une perspective clé pour analyser les dynamiques de marché.
Stochastic Models and Processes · 17. juin 2024
Comprenez l'interaction complexe entre le processus de Wiener \( W_t \) et son intégrale ∫ de 0 à t \( W_s \) ds. Ce produit stochastique nécessite des outils comme le lemme d'Itô pour analyser sa nature non linéaire. La covariation quadratique éclaire le comportement conjoint de ces processus, essentiel pour le pricing d'options exotiques, comme les options asiatiques.
Processus et Modèles Stochastiques · 12. novembre 2023
Le modèle de Hull-White valorise les dérivés de crédit comme les CDS en utilisant un taux de défaut stochastique. Il calcule les probabilités de survie et de défaut, ajuste les primes en fonction du risque, et utilise des données de marché pour estimer la valeur actuelle des paiements conditionnels liés aux défauts.
Pricing and Valuing Financial Instruments · 03. novembre 2023
Le modèle de Cheyette est un outil financier complexe pour prédire les mouvements des taux d'intérêt, prenant en compte la réversion à la moyenne et la volatilité variables dans le temps. Il est plus sophistiqué que des modèles plus simples comme celui de Vasicek en raison de ses paramètres détaillés, ce qui le rend robuste mais également plus intensif en calculs et moins couramment utilisé en pratique.
Processus et Modèles Stochastiques · 01. novembre 2023
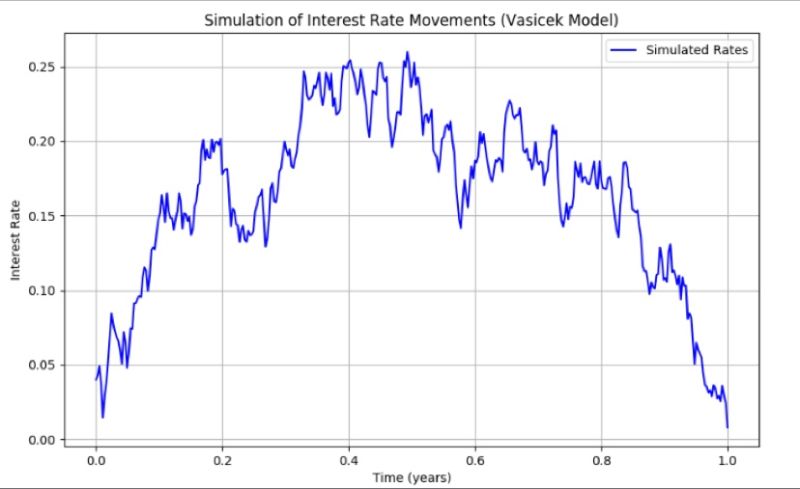
Découvrez dans cet article le modèle de Vasicek, un modèle mathématique permettant de modéliser les taux d'intérêt, à partir d'une équation différentielle stochastique. Il intègre les paramètres de retour à la moyenne, de volatilité et de vitesse de retour à cette moyenne. Il est largement utilisé pour simuler les mouvements des taux dans les marchés à revenu fixe. La formule principale est : dr(t) = κ(θ - r(t)) dt + σ dW(t).
Processus et Modèles Stochastiques · 29. juillet 2023
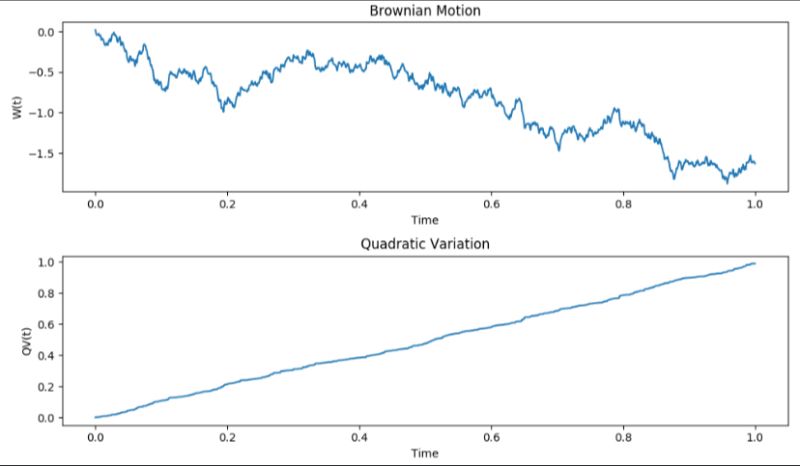
La variation quadratique en finance mesure la volatilité des mouvements de prix d’actifs, essentielle pour comprendre l'irrégularité des marchés et évaluer les risques dans le trading et la modélisation des options.
Processus et Modèles Stochastiques · 18. février 2023
Le terme d₁ dans la formule de Black-Scholes joue un rôle essentiel dans la tarification des options. Il englobe la position relative du prix de l’action par rapport au prix d’exercice, la valeur temporelle de l’argent et l'ajustement pour la volatilité. Cette formule capture l'ensemble des facteurs influençant la valeur d'une option.
Processus et Modèles Stochastiques · 04. février 2023
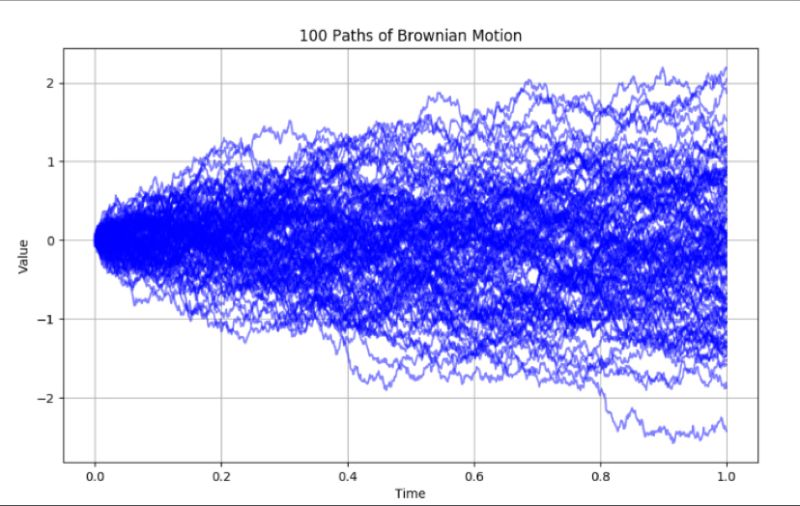
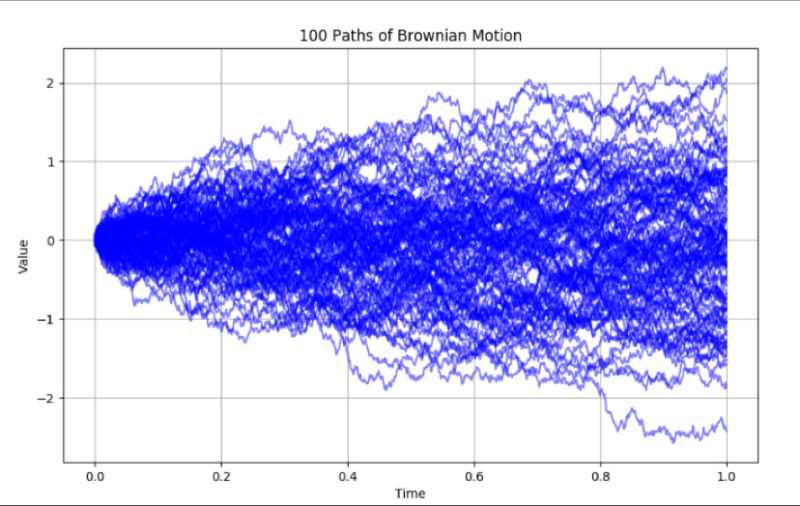
Le mouvement brownien modélise des trajectoires aléatoires en finance, avec une variance proportionnelle au temps. Son utilisation dans le modèle Black-Scholes permet de comprendre l’évolution des prix d’options et les risques associés sur des horizons temporels variables.
Stochastic Models and Processes · 04. février 2023
Brownian motion, a term often mentioned in the worlds of physics, mathematics, and finance, can be a puzzling concept to grasp. A seemingly random path that a particle traces in a liquid or gas medium, Brownian motion is often likened to the unpredictable movement of pollen particles in water. At its core, this stochastic process is governed by specific mathematical rules, one of the most intriguing being that its variance is directly proportional to time. Before delving into its variance-time...