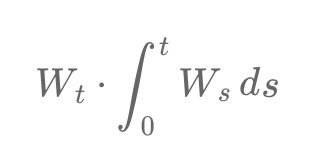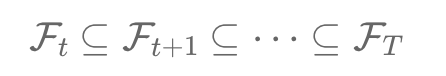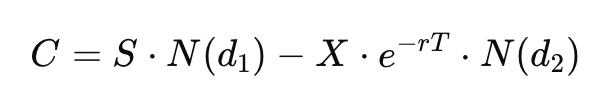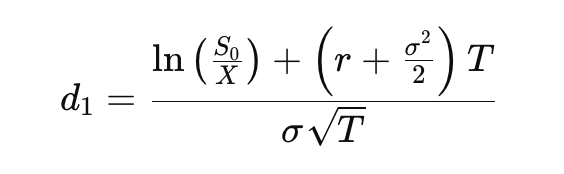Stochastic Models and Processes · 19. novembre 2023
Multiplying a Wiener process W_t by its integral creates a complex stochastic process, combining an instantaneous, "memoryless" state with its cumulative history. This nonlinear product, needing tools like Itô's lemma for analysis, reveals interactions between the current state and past values, crucial in financial mathematics for pricing path-dependent options.
Stochastic Models and Processes · 21. octobre 2023
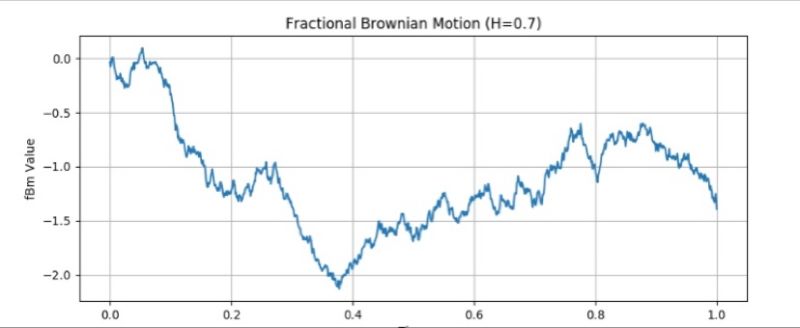
Fractional Brownian Motion (fBm) enriches classical Brownian motion by introducing the Hurst parameter (H), making it vital for modeling varying volatility in finance, physics, and beyond. With H dictating path roughness, fBm handles predictions in systems with long-range dependencies, aiding in asset volatility modeling and risk management. It's pivotal for understanding market behaviors and complex dynamics in diverse scientific fields.
Mathematical Principles and Quantitative Finance · 12. septembre 2023
Dive into the heart of finance with the sigma-algebra concept! Think of a deck of cards. Assigning probabilities, like drawing an Ace, means defining and combining events, and understanding their opposites. This structure, crucial in finance, ensures we consistently and meaningfully talk about events, especially in complex financial markets. As we track evolving information and model future possibilities, the sigma-algebra keeps our models from descending into chaos.
Stochastic Models and Processes · 29. juillet 2023
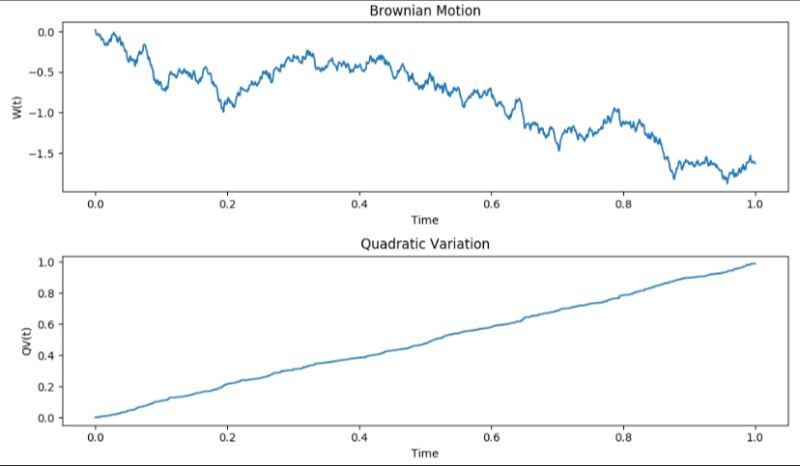
Explore the world of financial volatility with quadratic variation—a tool capturing asset "bumpiness". In finance, much like assessing a hiking trail's roughness, we gauge stock price fluctuations. With roots in Brownian motion, this metric offers insights into market behaviors, aiding predictions in high-frequency trading and refining the Black-Scholes model. Dive deep into market terrain with this crucial quantitative tool. #BrownianMotion #QuadraticVariation #QuantitativeFinance.
Stochastic Models and Processes · 20. mai 2023
In the Black-Scholes model, N(d1) and N(d2) are like gauges measuring the likelihood of different financial events. Imagine a game where you're guessing if a stock will reach a certain price. N(d1) is your best guess, factoring in the game's rules and odds. Meanwhile, N(d2) is about how much you'd ideally pay to play based on those odds. Together, they help determine an option's value. Simply, N(d1) gives the winning chance, and N(d2) gauges the cost. #OptionsExplained #BlackScholesModel
Stochastic Models and Processes · 18. février 2023
The d₁ term in the Black-Scholes model captures key factors of option pricing like stock price, strike price, volatility, and time. N(d₁) represents the option's delta, showing how sensitive its price is to the stock price. While often mistaken for the probability of the option ending in the money, this is actually the role of N(d₂). N(d₁) primarily reflects the option's sensitivity and hedge ratio.