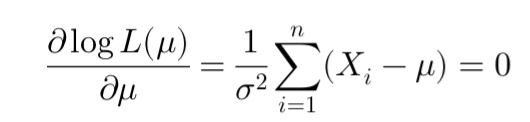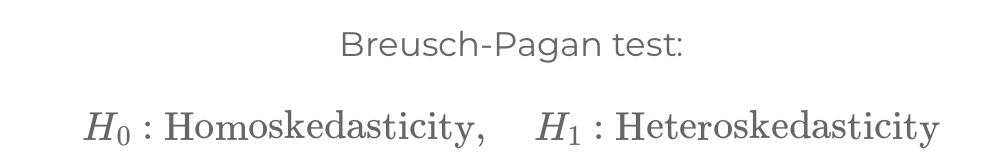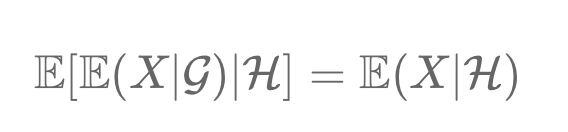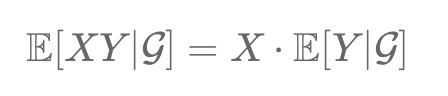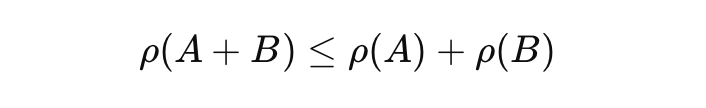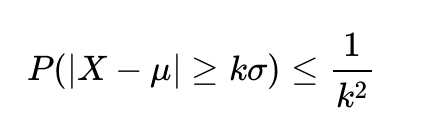Mathematical Principles and Quantitative Finance · 12. octobre 2024
Maximum Likelihood Estimation (MLE) is a statistical method used to estimate the parameters of a model based on observed data. It identifies the parameter values that maximize the likelihood of the observed data. MLE is widely used in finance, such as in estimating risk metrics like Value-at-Risk and Expected Shortfall by fitting models like the Generalized Pareto Distribution to extreme events.
Statistics · 14. février 2024
In regression analysis, heteroskedasticity and autocorrelation significantly impact model accuracy. Heteroskedasticity involves variable error variances, while autocorrelation means time-correlated residuals, both requiring tests like Breusch-Pagan and Durbin-Watson for detection and correction.
Stochastic Models and Processes · 19. novembre 2023
The Tower Property in probability theory simplifies conditional expectations. It states that refining information from a broader σ-algebra (𝒢) to a narrower one (H) yields the same expectation as directly using H. In finance, it means mid-year portfolio predictions remain valid regardless of additional end-year information. This principle aids in effective portfolio management and risk assessment.
Stochastic Models and Processes · 19. novembre 2023
Conditional expectation, 𝔼(X|𝒢), in probability theory, is defined within a probability space (Ω, F, P). It's the expected value of a random variable X given a sub-σ-algebra 𝒢 of F, offering insights based on additional information. This concept is vital in analyzing stochastic processes, aligning with the structure and constraints of 𝒢.
Mathematical Principles and Quantitative Finance · 14. novembre 2023
The Subadditivity Principle in risk management states that combined asset risks shouldn't surpass individual risks, highlighting diversification's role in reducing risk. This principle contrasts with Value at Risk (VaR), which often overlooks 'tail risks', making it non-subadditive. Conditional VaR (CVaR) addresses this by considering severe losses beyond VaR, ensuring a more accurate risk measure.
Mathematical Principles and Quantitative Finance · 13. novembre 2023
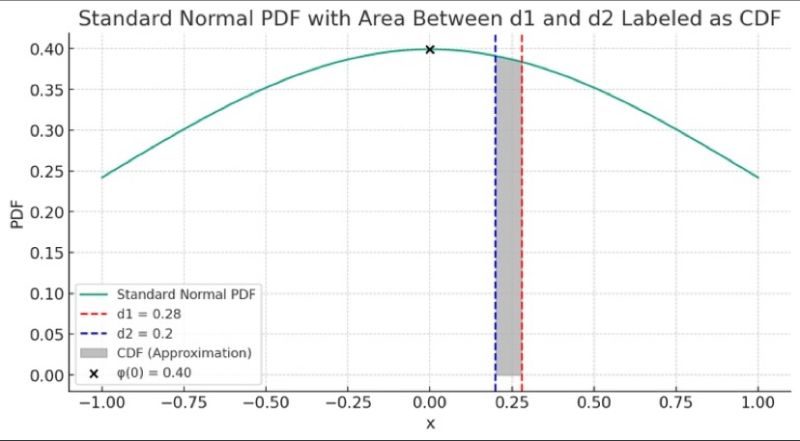
The article explains the connection between the Probability Density Function (PDF) and the Cumulative Distribution Function (CDF) in the context of the standard normal distribution. It highlights how the PDF measures the likelihood of a variable at a specific point, while the CDF calculates the probability of the variable being less than or equal to a given value.
Statistics · 11. novembre 2023
Chebyshev's inequality, vital in probability theory and finance, estimates the probability of a variable deviating from its mean by more than k standard deviations, capped at 1/k². Useful in finance for risk analysis and asset allocation, it applies to various distributions without needing a normal distribution assumption. However, it may overestimate extreme outcomes, leading to conservative strategies. #ChebyshevsInequality #QuantitativeFinance #RiskManagement #FinancialAnalysis
Mathematical Principles and Quantitative Finance · 21. octobre 2023
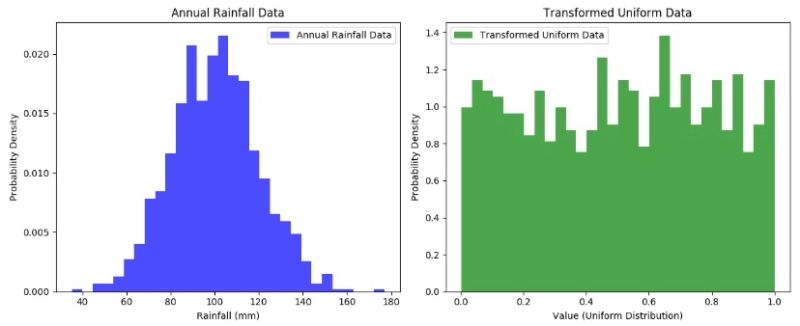
The Probability Integral Transform (PIT) converts a random variable into a uniform distribution using its cumulative distribution function (CDF). This helps assess model fit, compare datasets, and simplify simulations by enabling easy distribution transformations.
17. septembre 2023
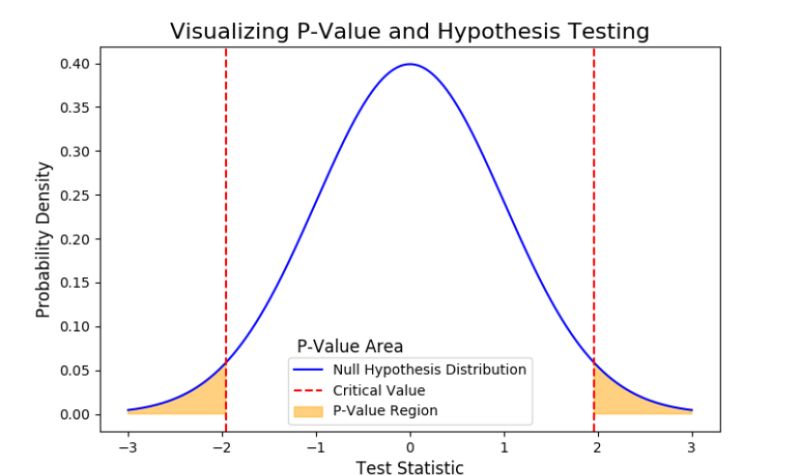
Unlock the mystery of copula in pairs trading and the p-value in hypothesis testing with our concise guide. Learn how copula aids in understanding dependencies and the p-value’s role in evaluating evidence against the null hypothesis, all explained simply. Stay informed and empowered in your trading and data analysis. #Copula #PValue #PairsTrading #DataAnalysis