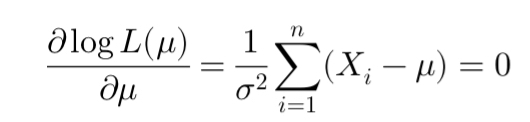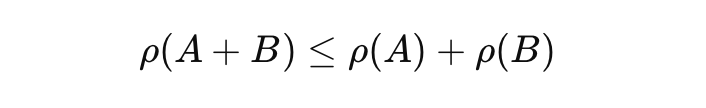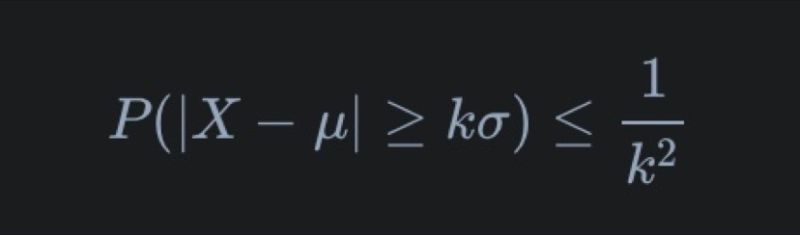Principes mathématiques et applications en finance · 12. octobre 2024
L'estimation par maximum de vraisemblance (EMV) est une méthode statistique utilisée pour estimer les paramètres d’un modèle à partir de données observées. Elle consiste à trouver les valeurs des paramètres qui maximisent la probabilité d’observer ces données. L'EMV est couramment utilisée en finance, par exemple pour estimer des mesures de risque comme la Value-at-Risk et l’Expected Shortfall en ajustant des modèles comme la distribution de Pareto généralisée aux événements extrêmes.
Mathematical Principles and Quantitative Finance · 13. novembre 2023
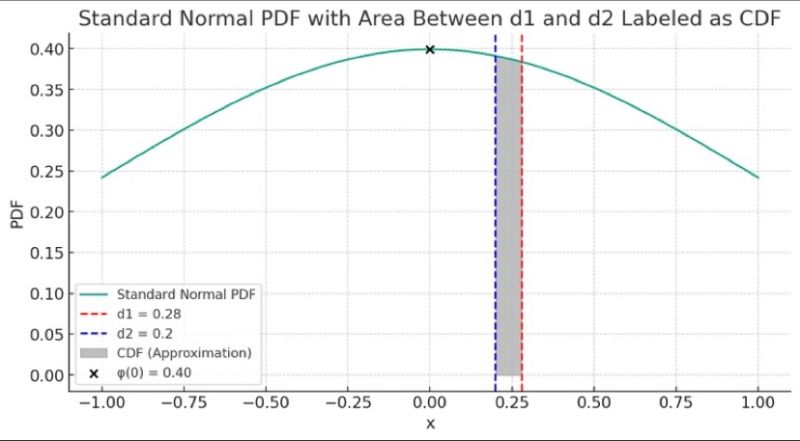
La PDF et la CDF sont essentielles pour modéliser la probabilité dans une distribution normale standard, utilisées en finance pour évaluer les options. Dans le modèle Black-Scholes, la relation entre N(d1) et N(d2) permet d’estimer la probabilité de variations de prix, facilitant la valorisation des options.
Mathematical Principles and Quantitative Finance · 11. novembre 2023
Chebyshev's inequality, vital in probability theory and finance, estimates the probability of a variable deviating from its mean by more than k standard deviations, capped at 1/k². Useful in finance for risk analysis and asset allocation, it applies to various distributions without needing a normal distribution assumption. However, it may overestimate extreme outcomes, leading to conservative strategies. #ChebyshevsInequality #QuantitativeFinance #RiskManagement #FinancialAnalysis