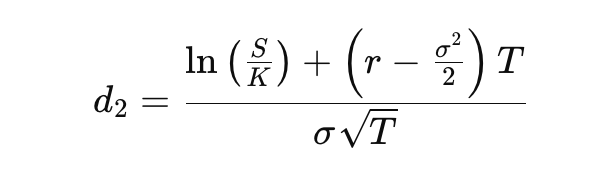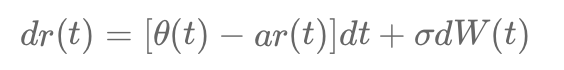Stochastic Models and Processes · 10. juin 2024
La formule de Black-Scholes pour une option d'achat calcule le prix de l'option en utilisant la probabilité d'exercer l'option, représentée par N(d2). Cette probabilité ajustée au risque assure une tarification sans arbitrage. Un N(d2) plus élevé signifie une probabilité accrue d'exercice de l'option, affectant le coût attendu et la valeur nette de l'option.
Mathematical Principles and Quantitative Finance · 10. juin 2024
Comprendre la distinction entre probabilités "du monde réel" et "neutres au risque" est essentiel en modélisation financière. Le théorème de Girsanov ajuste les processus stochastiques pour passer à une mesure neutre au risque, clé pour la tarification des dérivés. La dérivée de Radon-Nikodym facilite cette conversion. Des modèles comme HJM, CIR et Hull-White utilisent ce théorème pour garantir une tarification sans arbitrage.
Processus et Modèles Stochastiques · 12. novembre 2023
Le modèle de Hull-White valorise les dérivés de crédit comme les CDS en utilisant un taux de défaut stochastique. Il calcule les probabilités de survie et de défaut, ajuste les primes en fonction du risque, et utilise des données de marché pour estimer la valeur actuelle des paiements conditionnels liés aux défauts.