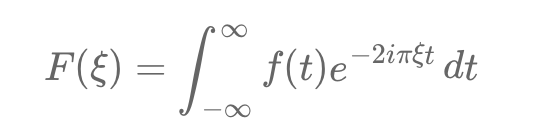Pricing and Valuing Financial Instruments · 30. septembre 2024

Option pricing, a key financial market challenge, relies on the Fourier transform to address complexities in valuation. An option grants the right to buy or sell an asset at a strike price, K, by expiration, T. The current price depends on the expected payoff, e.g., for a European call: max(S_T - K, 0). This is challenging as future asset prices follow complex stochastic processes. The Fourier transform simplifies this by converting payoff calculations from time to frequency domain.