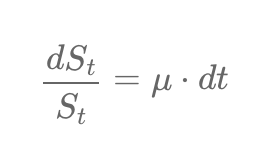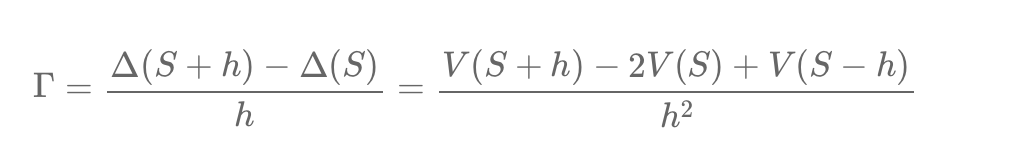13. novembre 2023
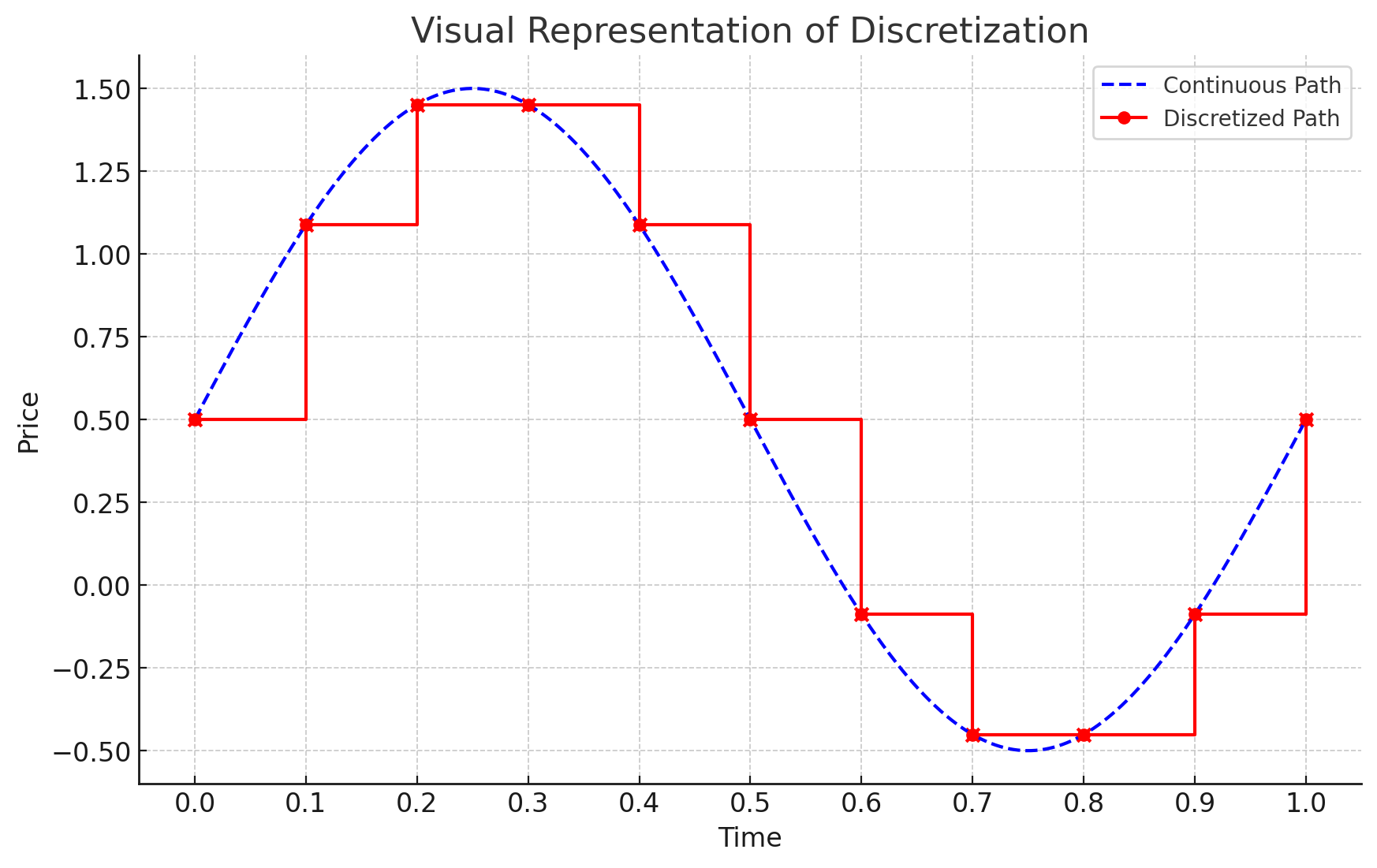
Discretization translates continuous financial models into numerically solvable steps, crucial for derivative pricing and risk management. It simplifies complex models, enabling simulations like Monte Carlo for exotic options while introducing some approximation error. #QuantitativeFinance #DerivativesPricing #NumericalMethods
Mathematical Principles and Quantitative Finance · 09. novembre 2023
An SPD matrix, with only non-negative eigenvalues, represents systems free from "negative energy" and ensures non-negative outcomes in various applications, including finance. It guarantees that any real vector, when applied to a quadratic form like portfolio variance, yields a non-negative result. SPD matrices are key in constructing risk models, pricing options, and in stochastic calculus, providing a reliable framework for financial analysis, optimization, and derivatives pricing.
Mathematical Principles and Quantitative Finance · 09. novembre 2023
Richardson extrapolation refines the accuracy of exotic option pricing in financial modeling. It adjusts for errors from numerical methods by using varied step sizes, leveraging the principle that error decreases quadratically with smaller steps, yielding more precise pricing estimates.
01. novembre 2023
The Crank-Nicolson Method, pivotal in quantitative finance, adeptly solves PDEs for option pricing and interest rate modeling. It splits time and space into grids, balancing calculations between current and next steps (implicit and explicit). It's stable and precise, essential for real-world financial scenarios.
Mathematical Principles and Quantitative Finance · 01. novembre 2023
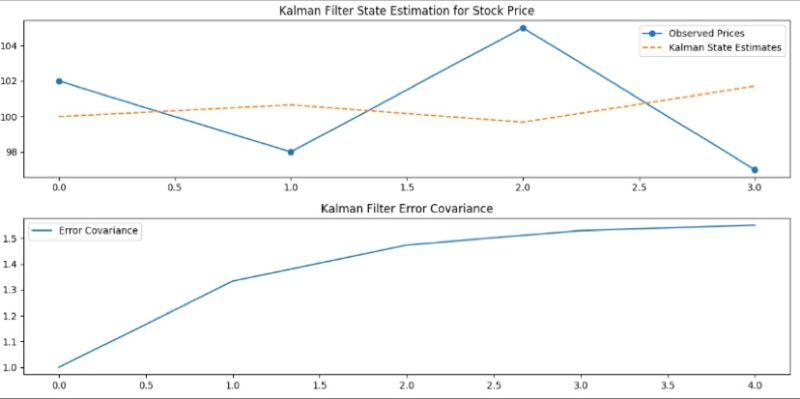
The Kalman filter refines estimates of financial states like stock prices from noisy data, crucial for asset tracking and trend analysis. It uses initial guesses and uncertainty measures, adjusting predictions with observed data over time. Kalman Gain balances predictions with actual trends for optimal estimation.
Principes mathématiques et applications en finance · 02. octobre 2023
Analytical methods offer exact solutions via mathematical formulas, ideal for simpler problems. E.g., Black-Scholes Model for option pricing. Numerical methods, like Monte Carlo simulations, provide approximate solutions for complex, real-world problems, but can be computationally intensive.
Mathematical Principles and Quantitative Finance · 08. septembre 2023
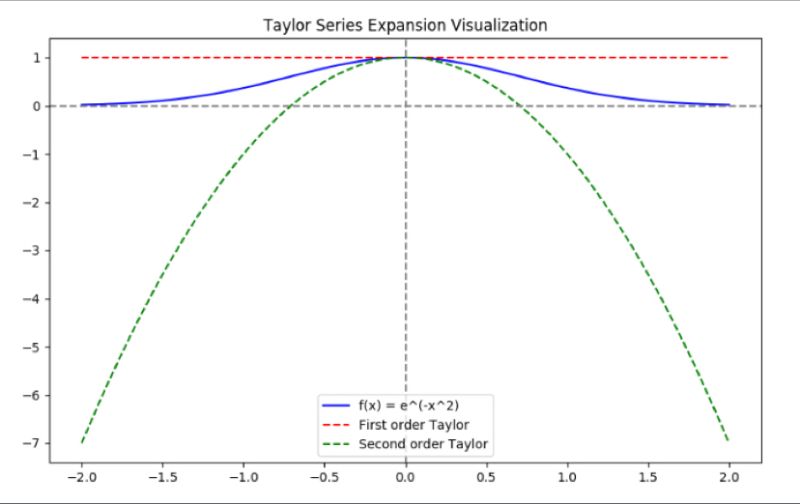
Taylor's expansion is an essential tool in quantitative finance for simplifying complex models, useful for quick decision-making, trading, and sensitivity analysis. It allows for the local approximation of a function through its derivatives, making it easier to understand its behavior.
22. juillet 2023
Differentiation helps forecast future stock prices. The equation dS/dt = μ * St indicates that a stock's price change is linked to a "drift" rate, μ. By adjusting and solving this equation, we get St = S₀ * e^(μt), a formula that predicts a stock's growth over time based on this drift. It's a mathematical way to gauge how stock prices evolve. #StockPricePrediction #Differentiation #FinancialModeling #DriftRate.
Mathematical Principles and Quantitative Finance · 18. mars 2023
Meet Alex, a derivatives trader at a major bank. Lately, the stock market has been fluctuating due to global events. Alex comes across a European put option on stock XYZ trading for $15. The stock itself is currently priced at $100, the option's strike price is $100, and it matures in a year. The generally accepted risk-free rate is 5%. Alex believes this put option might be overpriced. His theory is that even though the market is currently volatile, it might stabilize over the coming year. To...
Mathematical Principles and Quantitative Finance · 18. mars 2023
Navigating options is like hiking. To gauge a trail's steepness, you take small steps and check the height difference. This is the "slope" in hiking or the "delta" in options. But trails can vary in steepness, akin to the "gamma" in options. The finite difference method is our way of taking these small steps, offering insights into options without needing a full formula. Simply put, it's understanding changes step-by-step, just as in hiking. 🌄💹🚶♂️📊 #FiniteDifferenceMethod #OptionsInsight